Длины всех сторон двух подобных , но не равных друг другу треугольников целые числа . Чему может быть равен периметр большего , если в одном треугольнике есть длины 2 и 6 , а в другом треугольнике есть сторона длины 3 . Найдите все варианты
Объяснение:
1) В треугольнике с со сторонами 2, 6 , третья сторона может быть равной 5,6,7 согласно теореме о неравенстве сторон треугольника
( если х-третья сторона , то x+2>6 и 6+2>x ⇒ 4<х<8).
2)Тк треугольники подобны и известна одна сторона второго треугольника , то коэффициент подобия может быть равен
а) к=3:2=3/2 , или б) к=3:6=1/2.
Случай а) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(3/2)=9 и 2*(3/2)=3. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 9,9,3 , Р=21 ед.
Случай б) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(1/2)=3 и 2*(1/2)=1. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 3,3,1 , Р=7 ед.
ответ .Периметр большего треугольника 21 ед.
Теорема о неравенстве треугольника " каждая сторона треугольника всегда меньше сумме двух других его сторон."
a) высота боковой грани пирамиды - 6
б) сторона основания пирамиды - 12
c) площадь боковой поверхности пирамиды - 144
Объяснение:
Проведём перпендикуляр ОМ к стороне ромба ДС.
SO⊥OM ( SO - высота ромба, SO⊥(АСД), ОМ ∈(АСД) ⇒ SO⊥ОМ), ОМ⊥ДС ⇒ по "теореме о трёх перпендикулярах" SМ⊥ДС.
SМ - высотa боковой грани пирамиды
∠SМД - линейный угол двугранного угла при основании пирамиды.
∠SМД = 30° - по условию
а) Рассмотрим ΔSОМ(∠О=90°)
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. ⇒ SM = 2*SO = 2*3= 6 - высота боковой грани пирамиды
ОМ = SO / tg 30° =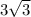
b) Рассмотрим ΔCОМ(∠М=90°).
Т.к. диагонали ромба являются биссектрисами его углов, то ∠ОСМ=∠ВСО=30°, ОМ - катет лежащий против угла в 30° ⇒
гипотенуза ОС=2*ОМ =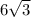
Рассмотрим ΔCОВ(∠О=90°).
ВС = ОС/ cos 30° =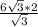 = 12 - Сторона основания пирамиды(все стороны ромба равны)
= 12 - Сторона основания пирамиды(все стороны ромба равны)
с) Площадь боковой поверхности пирамиды вычисляется по формуле:
Sб = 4 * S (ΔSDC)
S (ΔSDC) =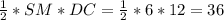
Sб = 4 * 36 = 144
Длины всех сторон двух подобных , но не равных друг другу треугольников целые числа . Чему может быть равен периметр большего , если в одном треугольнике есть длины 2 и 6 , а в другом треугольнике есть сторона длины 3 . Найдите все варианты
Объяснение:
1) В треугольнике с со сторонами 2, 6 , третья сторона может быть равной 5,6,7 согласно теореме о неравенстве сторон треугольника
( если х-третья сторона , то x+2>6 и 6+2>x ⇒ 4<х<8).
2)Тк треугольники подобны и известна одна сторона второго треугольника , то коэффициент подобия может быть равен
а) к=3:2=3/2 , или б) к=3:6=1/2.
Случай а) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(3/2)=9 и 2*(3/2)=3. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 9,9,3 , Р=21 ед.
Случай б) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(1/2)=3 и 2*(1/2)=1. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 3,3,1 , Р=7 ед.
ответ .Периметр большего треугольника 21 ед.
Теорема о неравенстве треугольника " каждая сторона треугольника всегда меньше сумме двух других его сторон."
orjabinina