до площини прямокутного трикутника abc (c = 90°) проведено пер­пендикуляр sb, sa = 13 см, b = 30°, ac = 5 см. знайдіть відстань від точки s до прямої ас.​

Диагональ делит прямоугольник на два равных прямоугольных треугольника. Рассмотрим ΔАСD (см. прикрепленный рисунок).

АС является гипотенузой в ΔАСD. АС = 3. Также известен острый угол в этом треугольнике ∠CAD = 37°.

Через синус и косинус найдем катеты треугольника АСD.

Синус острого угла в прямоугольном треугольнике - отношение противолежащего катета к гипотенузе.

Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета к гипотенузе.

CD и AD являются шириной и длиной в прямоугольника АВСD.

ответ: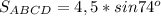 см².

Координаты середины отрезка, с концами в точках (х₁; у₁) и (х₂; у₂) находятся по формулам:

x = (x₁ + x₂)/2         y = (y₁ + y₂) /2

Получаем систему уравнений:

(x₁ + x₂)/2 = 5       | · 2

(x₂ + x₃)/2 = 2       | · 2

(x₁ + x₃)/2 = 2        | · 2

x₁ + x₂ = 10          (1)

x₂ + x₃ = 4           (2)

x₁ + x₃ = 4            (3)

Складываем все три уравнения, получаем:

2x₁  + 2x₂ + 2x₃ = 18        | : 2

x₁  + x₂ + x₃ = 9      

Теперь из полученного уравнения вычитаем каждое уравнение системы:

(1)   x₃ = - 1

(2)  x₁ = 5

(3)  x₂ = 5

Аналогично составляем и решаем вторую систему уравнений:

(y₁ + y₂)/2 = 2       | · 2

(y₂ + y₃)/2 = - 3    | · 2

(y₁ + y₃)/2 = 1        | · 2

y₁ + y₂ = 4          (1)

y₂ + y₃ = - 6       (2)

y₁ + y₃ = 2            (3)

Складываем все три уравнения, получаем:

2y₁  + 2y₂ + 2y₃ = 0        | : 2

y₁  + y₂ + y₃ = 0      

Теперь из полученного уравнения вычитаем каждое уравнение системы:

(1)   y₃ = - 4

(2)  y₁ = 6

(3)  y₂ = - 2

Координаты вершин:

(5 ; 6)       (5 ; - 2)        (- 1 ; - 4)