До кола з центром о проведено дотичну mn (m - точка дотику). знайти довжину відрізка mn, якщо on = 12см і кут nom = 30 градусів

Объяснение: ЗАДАНИЕ 1

треугольник ВОД- равнобедренный так как ОВ = ОД =радиусу. Поэтому угол ОВД=углу ОДВ. Найдём сумму этих углов, зная, что сумма углов треугольника составляет 180°. угол ОВД+угол ОДВ=

=180-80=100°. Так как углы равны, то:

угол ОВД=углу ОДВ=100÷2=50°

ответ: 50°

ЗАДАНИЕ 2

Если рассматривать условия обозначенных сторон, как отрезки, на которые окружность делит стороны треугольника, то:

МВ=ВN=4; NC=KC=8; MA=AK=5, как две касательные, которые соединяются в одной точке. Исходя из этого:

AB=MA+MB=5+4=9

BC=NC+BN=8+4=12

AC=AK+KC=5+8=13

P ∆ABC=AB+BC+AC=9+12+13=34

ответ: P=34

От себя добавлю, что: Если брать во внимание, что числа 4;5;8- это полные стороны треугольника, то нужно сложить их вместе и тогда получится периметр

12 см

Объяснение:

есть одно интересное свойство:

медиана прямоугольного треугольника есть радиусом описанной вокруг этого треугольника окружности, а диаметр такой окружности раден гипотенузе (это можно доказать из свойств угла, расположеного в окружности (прямой вписанный угол опирается на диаметр окружности) или как следствие теоремы, что центр описанной окружности вокруг прямоугольного треугольника лежит на середине гипотенузы)

Значит длина гипотенузы = 2*СD = 5 cm

один из катетов = 5-1 = 4 см

второй катет =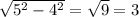 cм

P = 5+4+3 = 12 см