В равнобедренной трапеции диагональ является биссектрисой острого угла. Меньшее основание трапеции равно 17 см, а высота – 15 см. Чему равна площадь трапеции?
Объяснение:
1) АС-биссектриса ⇒ ∠ВАС=∠САD (*) .
Тк. ВС||AD, АС-секущая , то ∠САD=∠АСВ(**) как накрест лежащие.
Учтем (*) и (**) , получим ∠ВАС=АСВ ⇒ ΔАВС-равнобедренный и значит АВ=ВС= 17 см.
2) Пусть ВН ⊥AD, тогда ΔАВН-прямоугольный , по т. Пифагора АН=√(17²-15²)=8 (см) . По свойству равнобедренной трапеции
В равнобедренной трапеции диагональ является биссектрисой острого угла. Меньшее основание трапеции равно 17 см, а высота – 15 см. Чему равна площадь трапеции?
Объяснение:
1) АС-биссектриса ⇒ ∠ВАС=∠САD (*) .
Тк. ВС||AD, АС-секущая , то ∠САD=∠АСВ(**) как накрест лежащие.
Учтем (*) и (**) , получим ∠ВАС=АСВ ⇒ ΔАВС-равнобедренный и значит АВ=ВС= 17 см.
2) Пусть ВН ⊥AD, тогда ΔАВН-прямоугольный , по т. Пифагора АН=√(17²-15²)=8 (см) . По свойству равнобедренной трапеции
АН=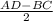 , 8 =
, 8 = 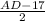 , 16=AD-17 , AD=33 см .
, 16=AD-17 , AD=33 см .
S=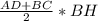 , S=
, S= 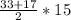 = 25*15=375 (cм²) .
= 25*15=375 (cм²) .
ответ: Пусть ∠ МВС = Ф, ∠ВМС=ω, ∠А=α, ∠АМВ=β, β+ω=180° как смежные углы и sinβ = sin(180°-ω) = sinω. В ΔАМВ по теореме синусов: sin∠C /АМ = sinω /4, в ΔВМС по т. синусов: sin∠C /3 = sinβ /6 ⇒
3/АМ = 6/4 ⇒ АМ = 2 ⇒ sinω = sinβ = 2*sin∠C
По теореме косинусов для ΔАМВ: АМ² = АВ² + ВМ²- 2*АВ*ВМ*cos∠C ⇒
2² = 4²+3² - 2*4*3*cos∠C ⇒ cos∠C = 21/24 = 7/8 ⇒
sin∠C = (1 - cos²∠C)^1/2 = √15/8, sinω = 2*sin∠C = √15/4, cosω=1/4
Ф = 180° - ω - ∠С ⇒ sin Ф = sin (ω+∠C) = sinω*cos∠C + cosω*sin∠C =
= √15/4 * 7/8 + 1/4 * √15/8 = 8√15/32 = √15/4 = sinω ⇒ по теореме синусов sinФ /МС = sinω /6⇒ МС = 6 ⇒ АС = АМ + МС = 2 + 6 = 8