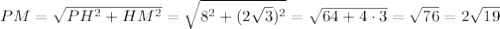для каждой геометрической фигуры,напишите номера рисунков,на которых она изображена с верным обозначением

для каждой геометрической фигуры,напишите номера рисунков,на которых она изображена с верным обознач

Показать ответ

Ответ:

agm7132

17.10.2022 07:03

Номер 9.

Расстояние от точки K до прямой а. Это длина перпендикуляра опушенного из K на a.

Большой треугольник равностороний т.к. его 3 стороны равны, значит биссиктрисы проведены из равных углов, то есть те 4 угла равны между собой. Из чего я делаю вывод, что маленький трекгольник равнобедренный и длина перпендикуляра из его вершины можно найти перемножив синус бокового угла и его боковую сторону, половина от угла равносторонего треугольника это 60/2=30. Значит расстояние: sin30*4=2 ну и вообще катет который лежит напротив угла 30 равняется половине гипотенузы (в прямоугольном треугольнике)

ответ: 2.

0,0(0 оценок)

Ответ:

sidorov26812

04.04.2023 13:33

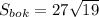
ответ: $S_{bok}=27\sqrt{19}$

Объяснение: РАВС - правильная треугольная пирамида, АВ=12 , РН=8, А₁В₁С₁║АВС .

АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды. ММ₁ – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости пересекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности

$\frac{PH_1}{PH}=\frac{PM_1}{PM}=\frac{A_1B_1}{AB}=\frac{1}{2}\\\\A_1B_1=\frac{AB}{2}=\frac{12}{2}=6$

Найдём НМ - радиус вписанной окружности в правильный треугольник:

$HM=r=\frac{AB\sqrt3}{6}=\frac{12\sqrt3}{6}=2\sqrt3$

Рассм. ΔРНМ: $PM=\sqrt{PH^2+HM^2}=\sqrt{8^2+(2\sqrt3)^2}=\sqrt{64+4\cdot 3}=\sqrt{76}=2\sqrt{19}$

$PM_1=\frac{1}{2}PM=\frac{1}{2}\cdot 2\sqrt{19}=\sqrt{19}\\\\MM_1=PM-PM_1=2\sqrt{19}-\sqrt{19}=\sqrt{19}\\\\S_{bok}=3\cdot \frac{AB+A_1B_1}{2}\cdot MM_1=3\cdot \frac{12+6}{2}\cdot \sqrt{19}=27\sqrt{19}$