Диагонали трапеции abcd с основаниями ad и bc пересекаются в точке о. а) докажите, что площади треугольников аов и соd равны. б) в треугольнике cod проведена высота oh = 6, причем ch = 3, угол doh в 2 раза больше угла coh. найдите площадь треугольника doh. с б

Показать ответ

Ответ:

gevorpilot

27.05.2020 17:25

Т.к. ОН - высота треугольника, то ОНС - прямоугольный. Найдём ОС по теореме Пифагора

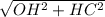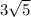
OC = $\sqrt{OH^{2}+HC^{2} }$ = $3\sqrt{5}$

Найдём синус и косинус угла НОС

sinHOC=HC/OC=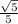 $\frac{\sqrt{5} }{5}$

cosHOC=OH/OC=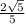 $\frac{2\sqrt{5} }{5}$

Т.к. по условию, угол DOH = 2 углам COH, то sinDOH=2*sinCOH*cosCOH

sinDOH=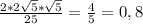 $\frac{2*2\sqrt{5}*\sqrt{5} }{25} =\frac{4}{5}=0,8$

Из основного тригонометрического тождества найдём cosDOH

$cosDOH=\sqrt{1-sin^{2}DOH } =0,6$

cosDOH=OH/OD ==> OD=OH/cosDOH=6/0,6=10

Тогда DH из теоремы Пифагора равна - 8

Sdoh=0,5*OH*DH=0,5*6*8=24

ответ 24

0,0(0 оценок)

Популярные вопросы: Геометрия

KsenyaKnyazeva1

01.09.2020 17:28

Через точку М яка не належить між двома паралельними площинами альфа і бета проведено дві прямі, які перетинають альфу в точках А1, і А2, а площину бета в точках В1 і В2...

stf74149

28.10.2020 01:15

В прямоугольный треугольник с катетами 3 ед. изм. и 3 ед. изм. вписан квадрат, имеющий с треугольником общий прямой угол. Вычисли периметр квадрата. Периметр квадрата равен...

GNA14

24.07.2021 07:36

Обчисли гострий кут ромба, якщо сума двох кутів цього ромба дорівнює 250°. Відповідь: гострий кут ромба дорівнює °....

vaneeva06

25.08.2022 16:42

Найдите площадь трапеции abcd с основаниями ab и cd если угол d 30 градусов ab=2см cd=8см...

Болыс111

28.05.2020 05:36

Объясните отрезки ab и cd являются окружности. найдите длину хорды cd,если ab =8,а расстояние от центра окружности до хорд ab и cd равны соответственно 3 и 4....

00099000

28.05.2020 05:36

Втреугольнике авс на высоте bf отмечена точка о, такая сто ао=ос. расстояние от точки о до стороны ав равно 4 см, а до стороны ас - 7 см. найдите расстояние от точки о до...

bekahasanov

28.05.2020 05:36

Решить в равнобедренном треугольнике abc основание ac и медиана ap равны по 6см; o-пересечения медиан треугольника.найдите периметр треугольника aoc....

Aye03

16.06.2021 09:34

Задание 1 ( ). На прямой отмечены точки A, B, C и D. Точка С - середина отрезка BD; точка В – середина отрезка AD. Определите длину отрезка AD, если AC = 12 см. A ор С D...

megan99

29.10.2022 07:16

У трикутнику АВС, висота, опущена з вершини В, перетинає сторону АС у точці Н, а бісектриса кута В перетинає АС у точці М. ∠АВН = 23°, ∠ВМА = 64°. Знайдіть кути трикутника...

natashavoropaeva

16.08.2021 23:29

На рисунке прямые AB и CD пересечены секущими MN и RP Угол MOB равен a, угол OPD равен 1/2a и OR - биссектриса угла MOB. Определи, параллельны ли прямые AB и...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку