1. Известно, что треугольник с искомыми сторонами подобен исходному, то есть все соответственные элементы у треугольников соотносятся как коэффициент подобия.
Пусть коэффициент подобия равен . Тогда стороны второго треугольника равны . А их сумма, то есть периметр, рана 58,5 см.
Имеем уравнение
ответ: 13,5 см, 18 см, 27 см.
2. Сумма углов треугольника равна 180°. Третий угол равен 180°-(54°+18°)=108°
Далее, биссектриса делит угол пополам, то тупой угол будет разбит на два угла по 108°/2=54°
Получится два треугольника (рисунок приложен)
Рассмотрим треугольник, в котором присутствует угол 18° из исходного треугольника (левый на рисунке). Второй угол равен 54°. Но и в исходном треугольнике есть углы 18° и 54°, а это означает, что этот отсеченный треугольник подобен исходному треугольнику (по двум углам). Второй отсеченный треугольник, кстати, является равнобедренным (имеет два угла по 54°).
Для начала, найдём координату центра окружности. Для этого воспользуемся соответствующей формулой:
О(х1+х2/2;у1+у2/2). Подставим числа и получим:
О(0+6/2;2-2/2)
О(3;0). Для того, чтобы написать уравнение окружности нам не хватает её радиуса. Найдём сначала длину диаметра, а затем выразим радиус. Теперь воспользуемся другой формулой:
d=корень из (х2-х1)^2+(у2-у1)^2. Получим:
d= корень из (6-3)^2+(-2-0)^2= корень из 13. Теперь, пришло время составить уравнение окружности. Оно будет выглядеть так:
(х-х0)^2+(у--у0)^2=r^2. Это оно в общем виде, а теперь подставим числа и получим:
1. Известно, что треугольник с искомыми сторонами подобен исходному, то есть все соответственные элементы у треугольников соотносятся как коэффициент подобия.
Пусть коэффициент подобия равен
. Тогда стороны второго треугольника равны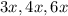 
. А их сумма, то есть периметр, рана 58,5 см.
Имеем уравнение
ответ: 13,5 см, 18 см, 27 см.
2. Сумма углов треугольника равна 180°. Третий угол равен 180°-(54°+18°)=108°
Далее, биссектриса делит угол пополам, то тупой угол будет разбит на два угла по 108°/2=54°
Получится два треугольника (рисунок приложен)
Рассмотрим треугольник, в котором присутствует угол 18° из исходного треугольника (левый на рисунке). Второй угол равен 54°. Но и в исходном треугольнике есть углы 18° и 54°, а это означает, что этот отсеченный треугольник подобен исходному треугольнику (по двум углам). Второй отсеченный треугольник, кстати, является равнобедренным (имеет два угла по 54°).
Для начала, найдём координату центра окружности. Для этого воспользуемся соответствующей формулой:
О(х1+х2/2;у1+у2/2). Подставим числа и получим:
О(0+6/2;2-2/2)
О(3;0). Для того, чтобы написать уравнение окружности нам не хватает её радиуса. Найдём сначала длину диаметра, а затем выразим радиус. Теперь воспользуемся другой формулой:
d=корень из (х2-х1)^2+(у2-у1)^2. Получим:
d= корень из (6-3)^2+(-2-0)^2= корень из 13. Теперь, пришло время составить уравнение окружности. Оно будет выглядеть так:
(х-х0)^2+(у--у0)^2=r^2. Это оно в общем виде, а теперь подставим числа и получим:
(х-3)^2+у^2=13. Это и есть ответ.