Даны точки А(2;4) и В(-4;-2)

1) Найти координаты вектора АВ,

2) Найти длину отрезка АВ,

3) Найти длину вектора АВ,

4) Найти координаты точки М – середины отрезка АВ,

5) Найти уравнение прямой , проходящей через точки А и В,

6) Написать уравнение окружности с центром в точке А, проходящей через точку В.​

Объяснение:

Не уверен, но вариант такой:

Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.

Тогда угол AKC 180-90-45 = 45 град.

Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.

Для прямоугольного треугольника АКС получаем

квадрат АК= квадрату АС + квадрат КС

квадрат АК = квадрат ВК + квадрат ВК

АК = ВК х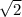

1. Пусть х - боковая сторона, так как это равнобедренный треугольник, то боковые стороны равны, значить х+х - сумма боковых сторон треугольника, тогда 4+х - основание.

Т.К. периметр треугольника равен 46 см , составляю уравнение:

х+х+х+4=46

3х=42

х=14

Боковые стороны равны 14см , значит основание равно 14+4=18 см

ответ: боковые стороны равны 14 см, основание равно 18 см.

2. Т.к. треугольник равнобедренный, то биссектриса является медианой (по свойству), следовательно АД=СД.

Рассмотрим треугольники АВД и СВД:

1)АД=СД(по доказанному)

2)уголА=уголС(по свойству равнобедренного треугольника)

3)АВ=АС по определению

следовательно треугольник АВД=СВД по двум сторонам и углу между ними.

Так как треугольники равны, то их периметр тоже равен, значит сумма сторон треугольника АВД , которые не являются биссектрисой угла 68:2=34(см).

Следовательно периметр треугольника АВД равен 34+17 = 51(см)

ответ: периметр АВД=51 см.

3.(К данной задаче выполню рисунок)

Рассмотрим треугольники ДАС и ЕСА:

1)Сторона АС - общая.

2)углы А=С (по свойству равнобедренного треугольника)

3)ДА=ЕС(по условию)

Треугольники равны по двум сторонам и углу между ними.

Следовательно ДС=ЕА (как соответственные элементы равных треугольников.