Даны точки А(0; 0), В(1; 1), С(0; 2) D(-1;1). Докажите, что четырехугольник ABCD –квадрат
2. Найдите площадь круга, если площадь вписанного в неё правильного шестиугольника равна 72 .
3. Найдите координаты вектора МК, если М(8; 3), К(2; -4).
{-4; -6}; 2) {-6; -7}; 3) {-7; 0}; 4) {-4; 0}
4. Какие из следующих уравнений задают окружность
1) (x +10)2+ (y +1)2 = 25; 2) 3 x2 + 4y2 = 9; 3) 2x2 +4 y2 = 0; 4) x2 + y2 +2= 0

На сколько я понял требуется решить только первую задачу.

Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.

Найти радиус описанной около ABCD.

Пусть AC∩BD=F и пусть ∠FAB=α.

Вокруг равнобедренной трапеции всегда можно описать окружность!

ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.

В ΔAFD:

∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.

В прямоугольном ΔAFB:

AF=AB·cosα=7√2·cosα см

BF=AB·sinα=7√2·sinα см

В ΔABD:

BD=BF+FD=BF+AF=7√2·(sinα+cosα) см

∠BAD=α+45°

Вокруг ΔABD описана таже окружность, что и вокруг трапеции.

По теореме синусов: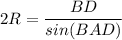 , где R - радиус описанной.

ответ: 7 см.

В прямоугольнике ABCD из вершины B опущен перпендикуляр BK на диагональ AC. Найдите площадь прямоугольника, если BK = 4 , KC= 8    

"Решение"

* * * Cразу можно  написать:  BC² = AC *KC _ пропорциональные отрезки в прямоугольном треугольнике  * * *   A  если . . .

ΔBKC ~ΔABC  ⇒ BK/AB  =    BC / AC = KC/BC ⇔  BC² = AC *KC , но

BC² = BK²+ KC² =4² +8² =80 (теорема Пифагора)

80 =AC*8 ⇒AC =10    

BK/AB = BC / AC ⇔  AB *BC = AC*BK ⇔ S(ABCD) = AC*BK =10*4= 40                        (ед. площади)        ||  S(ABCD) =2*AC*BK/2 =2S(ABC) ||

S(ABCD)  = AC*BK =10*4= 40   (ед. площади)