Даны окружности радиусов 2 и 4, расстояние между центрами которых равно 16. Найдите множество середин всех отрезков, у которых один конец на первой окружности, а другой - на второй.
Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?
Объяснение:
Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).
Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?
Объяснение:
Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).
S(ABC)=S( PAB)+S(PBC)+S(PAC).
S(ABC)=S(равн. тр)=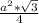 =
=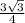 ,
,
S( PAB)=1/2*a*h=1/2*√3*x,
S(PBC)=1/2*a*h=1/2*√3*y,
S(PAC)=1/2*a*h=1/2*√3*z.
x+y+z=1,5
Любая линейная функция выражается формулой y = kx + b. Подставим известные нам значения x и y из точек в эту формулу и составим систему:
Вычтем из второго уравнения первое и найдём k:
Подставим найденный k в любое уравнение линейной функции из системы, чтобы найти b:
Таким образом, уравнение первой линейной функции f (x) выглядит как y = -1x + 0, или, упрощая, y = - x.
Повторим те же действия с точками функции g (x). Составляем систему:
На этот раз проще будет сначала найти b, так как это можно сделать сложением двух уравнений:
Подставляем в уравнение из системы:
Таким образом, уравнение второй линейной функции g (x) выглядит как y = 2x + 3.
Чтобы найти точку пересечения графиков линейных функций, необходимо приравнять их формулы друг к другу, чтобы найти общую абсциссу. Получаем:
Найдём значение ординаты y в точке пересечения по любой из формул:
Таким образом, графики функций f (x) и g (x) пересекаются в точке (- 1; 1).