Геометрия: Даны координаты точек: А (6:8) В (-3;8) С (6;-1) D (2;-6)

Фактически задача сводится к нахождению координат вектора CD. Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C. Условие перпендикулярности - косинус угла между векторами CD и AB равен нулю. Формула косинуса угла между векторами - AB={-1+5;4-1}={4;3} CD={x2-3;y2-2} Составим уравнение прямой АВ: (*) Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим: 4(x2-3)+3(y2-2)=0 Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*). Решаем полученную...

Даны координаты точек:
А (6:8)
В (-3;8)
С (6;-1)
D (2;-6)

Даны координаты точек: А (6:8) В (-3;8) С (6;-1) D (2;-6)

Показать ответ

Ответ:

Лейла0044

30.05.2021 02:31

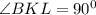Что- то мало баллов. :) Обозначим за с=АВ=10 см меньшую хорду (с - так как лежит напротив угла С). а=ВС=12 см - большую сторону (а - так как лежит напротив угла А). Неизвестной останется только сторона b=АС (b - так как лежит напротив угла В). Тогда АВС - треугольник, вписанный в окружность. Пусть AL=LB - середина стороны AB. Точка К - принадлежит стороне BC, причем BK=3 см и $\angle BKL=90^0$ согласно условию задачи. Тогда треугольник BKL - прямоугольный. Нетрудно понять по теореме Пифагора, что сторона

$LK=\sqrt{LB^2-BK^2}$

$LK=\sqrt{5^2-3^2}$

$LK=\sqrt{25-9}$

$LK=\sqrt{16}$

LK=4.

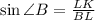
Тогда по определению $\sin\angle B=\frac{LK}{BL}$

$\sin\angle B=\frac{4}{5}$ .

Чтобы найти радиус описанной окружности воспользуемся частью теоремы синусов

$\frac{b}{\sin\angle B}=2R$

$\frac{b}{\frac{4}{5}}=2R$

5b=8R

$R=\frac{5b}{8}\quad (1)$

Чтобы вычислить b=AC придется применить теорему косинусов.

$AC^2=AB^2+BC^2-2*AB*BC*\cos(\angle B)$

$AC^2=10^2+12^2-2*10*12*\cos(\angle B)$

$AC^2=100+144-240*\cos(\angle B)$

По определению

$\cos(\angle B)=\frac{BK}{LB}$

$\cos(\angle B)=\frac{3}{5}$

$AC^2=100+144-240*\frac{3}{5}$

AC^2=100+144-144

AC^2=100

AC=10

b=10.

Подставляю в формулу (1)

$R=\frac{5*10}{8}$

$R=\frac{25}{4}$

R=6,25

ответ: радиус окружности равен 6,25 см.

0,0(0 оценок)

Ответ:

дашуся4

19.04.2020 15:19

Фактически задача сводится к нахождению координат вектора CD.

Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.

Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.

Формула косинуса угла между векторами -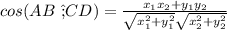 $cos(AB\ \^;CD)=\frac{x_{1}x_{2}+y_{1}y_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}}\sqrt{x_{2}^{2}+y_{2}^{2}}}$

AB={-1+5;4-1}={4;3}

CD={x2-3;y2-2}

Составим уравнение прямой АВ: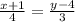 $\frac{x+1}{4}=\frac{y-4}{3}$ (*)

Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:

4(x2-3)+3(y2-2)=0

Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).

Решаем полученную систему уравнений.

$\left \{ {{4(x2-3)+3(y2-2)=0} \atop {\frac{x2+1}{4}=\frac{y2-4}{3}}} \right.$

Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.

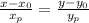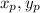Оно выглядит так: $\frac{x-x_{0}}{x_{p}}=\frac{y-y_{0}}{y_{p}}$ , где $x_{p}, y_{p}$ - координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)