По условию АВ=14, АС=16, ВС=10 В любом треугольнике против наибольшего угла лежит наибольшая сторона, а против наименьшего угла лежит наименьшая сторона. Значит в нашем треугольнике минимальным углом является угол А.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. BC²= AB² + AC² – 2AB · AC cos ∠А. 10²=14²+16²-2*14*16 cos ∠А 100=196+256-448cos ∠А 448cos ∠А=196+256-100 448cos ∠А=352 cos ∠А=352/448 cos ∠А=11/14 По таблице косинусов ∠А≈38°
В любом треугольнике против наибольшего угла лежит наибольшая сторона, а против наименьшего угла лежит наименьшая сторона.
Значит в нашем треугольнике минимальным углом является угол А.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
BC²= AB² + AC² – 2AB · AC cos ∠А.
10²=14²+16²-2*14*16 cos ∠А
100=196+256-448cos ∠А
448cos ∠А=196+256-100
448cos ∠А=352
cos ∠А=352/448
cos ∠А=11/14
По таблице косинусов ∠А≈38°
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD=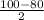 =10°.
=10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD=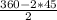 =135°
=135°