АВ=ВС, т.к. треугольник равнобедренный, а АС - основание. ВК=2, АК=8, тогда, АВ=10. Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов. АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16. В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6. Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.
Вариант 1.
1.
Для начала найдём один из отрезков, полученным, делением гипотенузы высотою: отрезок BD.
Так как это высота, то отрезок образует 2 прямых угла: <BDA; <ADC.
Тоесть образуется 2 прямоугольных треугольника: ΔBDA; ΔADC.
По теореме Пифагора — BC равен:
Чтобы найти всю гипотенузу BC — вычислим оставшийся отрезок DC.
Для этого нам нужна одна из формул вычисления высоты прямоугольного треугольника:
DC = 9; BD = 16 => BC = 9+16 = 25см.
По теореме Пифагора, AC равен:
Косинус угла равен отношению прилежащего катета к гипотенузе, то есть:
Вывод: AC = 21.9см; cos(<C) = 0.876.
2.
Для начала найдём оставшийся стороны паралеллограмма: BD & AD, которые друг другу равны.
Так как BD — перпендикулярен стороне AD — то он образует прямой угол с этой сторон, тоесть: ΔADB — прямоугольный.
Формула вычисления стороны BD, зная угол A, и гипотенузу AB: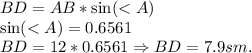
Осталось найти сторону AD (по теореме Пифагора), на которой проведена высота BD, чтобы потом найти площадь:
Теперь, формула вычисления площад параллелограмма такова: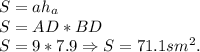
Вывод: S = 71.1см².