Дано:
M N = 7 м;
угол MNO = 60°.
Найти:
KN =
м.​

Из точки находящийся на расстоянии корень с 3 см от плоскости проведен к этой плоскости две наклонные которые наклонены к плоскости под углами 45° и 60°. Найдите расстояние между основаниями наклонных если наклонные перпендикулярны.

Объяснение:

Т.к ОМ -расстояние и ОМ⊥α, то ОМ⊥ОВ и ОМ⊥ОА .

ΔОМА-прямоугольный ,∠ОАМ=45° ⇒ ∠ОМА=45° поэтому

ОМ=ОА=√3 см . Найдем по т. Пифагора МА=√(√3²+√3²)=√6 (см).

ΔОМВ -прямоугольный, ∠ОВМ=60° , sin 60=OM/MB ,√3/2=√3/МВ , МВ=2 см.

ΔОМВ -прямоугольный,по т. Пифагора АВ=√(МА²+МВ²)=√(6+4)=√10 (см)

Точка S находится на одном расстоянии от всех вершин правильного треугольника со стороной 2 корня из 3 см и відалена от плоскости треугольника на корень из 3 см найдите расстояние от точки S до вершины треугольника.

Объяснение:

Т.к. точка S находится на одном расстоянии от всех вершин правильного треугольника, то SA=SB=SC.

Расстояние от  S  до плоскости ( АВС) √3 см⇒SO⊥(АВС). Тогда прямоугольные треугольники равны по катету (SO-общий) и гипотенузе ( SA=SB=SC.)  ΔSOA=ΔSOB=ΔSOC ⇒ОА=ОВ=ОС и значит О-центр описанной окружности около правильного ΔАВС и ОА=ОВ=ОС=R =  ,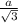

R =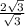 =2 (см)

ΔSOA- прямоугольный , по т. Пифагора SA= √(2²+√3²)=√7 (cм)