Дано, что треугольник ABC - равнобедренный. Основание AB треугольника равно 1/10 боковой стороны треугольника. Периметр треугольника ABC равен 231 дм. Вычисли стороны треугольника.

Показать ответ

Ответ:

Retyyyghiop

09.04.2023 19:30

Если боковые рёбра равны, то вершины проецируется в центр описанной окружности (Это следует из равенства 3 треугольников по общему катету-высота пирамиды и гипотенузе-боковому ребру пирамиды). Тогда боковое ребро можно найти по теореме пифагора, где ребро - гипотенуза, радиус описанной окружности и высота пирамиды - катеты.

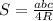
Для треугольника: $S=\frac{abc}{4R}$

Где a,b,c - стороны; R-радиус описанной; S-площадь.

А площадь можно найти через формулу Герона.

$S=\sqrt{p(p-a)(p-b)(p-c)}$

Где a,b,c-стороны треугольника; S-его площадь; p-полупериметр (половина от периметра).

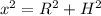
А боковой ребро мы найдём: x^2=R^2+H^2

Где x-боковое ребро; R-радиус описанной; H-высота пирамиды.

$p=\frac{16+63+65}{2}=\frac{144}{2}=72\\S=\sqrt{72*(72-16)(72-63)(72-65)}=\sqrt{72*56*9*7}=\\\sqrt{9^2*8^2*7^2}=7*8*9\\R=\frac{abc}{4S}=\frac{16*63*65}{4*7*8*9}=\frac{65}{2}=32.5\\x^2=32.5^2+130^2=32.5^2+(32.5*4)^2=32.5^2(1+4^2)=32.5^2*17\\x=32.5*\sqrt{17}$

ответ: 32.5*√17.

Для ясности внизу рисунок.

Дана треугольная пирамида.стороны основания равный 13,63,65.высота пирамиды равна 130.все боковые рё

0,0(0 оценок)

Ответ:

asadhfdgj

10.10.2022 15:15

Объяснение:

Боковыми гранями правильной усеченной пирамиды являются равные равнобедренные трапеции. Для нахождения площади боковой поверхности нужно найти высоту этих трапеций.

Проведем из вершин В и В1 оснований пирамиды высоты (медианы) ВН и В1М. В треугольнике АВС т.О - центр вписанной окружности и делит ВН в отношении 2:1, считая от вершины (по свойству медиан). ОН=ВН:3=АВ•sin60°:6. ОH=6•√3:2):3.=√3

Аналогично находим длину МО1 в меньшем основании А1В1С1. Отрезок МО1=(√3)/3.

Из т.М опустим перпендикуляр МК на ОН.

НК= НО-МО1=√3-(√3)/3= (2√3)/3

МК - катет прямоугольного треугольника МКН с гипотенузой МН=НК:cos ∠МНК=[(2√3):3]:1/2=4/√3 .

По т. о 3х- перпендикулярах МН⊥АС и является высотой трапеции АА1С1С.

Площадь боковой поверхности данной пирамиды Ѕ(ус.пир.)=3•Ѕ(АА1С1С)=3•МН•(А1С1+АС):2.

Ѕ(ус.пир.)=3•(4:√3)•8:2=16√3 см²

————

Для нахождения высоты полной пирамиды РАВС, из которой получена данная усеченная пирамида, рассмотрим ∆ РОН и ∆ МНК. Они прямоугольные, имеют общий острый угол при вершине Н, ⇒

∆ РОН ~∆ МНК. k=НО:НК=√3:(2√3)/3=3/2

РО:МК=3/2.

МК=МН•sin60°=(4/√3 )•√3/2=2 см ⇒

PO=3 см