Угол равный 60градусов будет лежать против стороны равной 5 см, т. к. этот угол меньше 90 градусов. значит второй угол образованный этими диагоналями равен 120 гр. (т. к. вместе они образуют развернутый угол) пусть прямоугольник будет АВСД, точка пересечения диагоналей О, тогда в треугольнике АОВ опускаем высоту ОК, т. к. треугольник равносторонний, то ОК будет и медианой и биссектрисой полученный угол КОА будет равен 30 гр. а отрезки ВК и АК равны по 2,5 см. По правилу "сторона лежащая против угла в 30 гр равна половине гипотенузы"(в треугольнике АОК) следует, что гипотенуза т. е. сторона АО равна двум длинам стороны АК, т. е. АО равна 5 см. У диагонали АС точка О является ее центром симметрии, значит АС равна 10 см Теперь рассмотрим треугольник АСВ, в котором нам известно: АВ рана 5 см, АС = 10 см. Треугольник прямоугольный. По теореме Пифагора сторона ВС2 = АС2(в квадрате) - АВ2. отсюда следует ВС равна 5корень из5 площадь прямоугольника равна АВ умножить на ВС, т. е. выходит S=5*5 корень из 5=25к орень из 5
значит второй угол образованный этими диагоналями равен 120 гр. (т. к. вместе они образуют развернутый угол)
пусть прямоугольник будет АВСД, точка пересечения диагоналей О,
тогда в треугольнике АОВ опускаем высоту ОК, т. к. треугольник равносторонний, то ОК будет и медианой и биссектрисой
полученный угол КОА будет равен 30 гр. а отрезки ВК и АК равны по 2,5 см.
По правилу "сторона лежащая против угла в 30 гр равна половине гипотенузы"(в треугольнике АОК) следует, что гипотенуза т. е. сторона АО равна двум длинам стороны АК, т. е. АО равна 5 см.
У диагонали АС точка О является ее центром симметрии, значит АС равна 10 см
Теперь рассмотрим треугольник АСВ, в котором нам известно: АВ рана 5 см, АС = 10 см. Треугольник прямоугольный.
По теореме Пифагора сторона ВС2 = АС2(в квадрате) - АВ2. отсюда следует ВС равна 5корень из5
площадь прямоугольника равна АВ умножить на ВС, т. е. выходит S=5*5 корень из 5=25к орень из 5
Объяснение:
1.
1)формула периметра та площі паралелограма
P=2(a+b)
S=ah, h - висота
2)формула периметра та площі прямокутника
P=2(a+b)
S=a* b
3)формула периметра та площі ромба
P=4a
S=ah
4)формула периметра та площі квадрата
P=4a
S=a²
2.
1. Знайдіть площу квадрата якщо його периметр становить 80см
Розвязання
периметр квадрата P=4a, знаходимо а
80=4а, а=80/4=20см - одна сторона квадрата
площа квадрата S=a² ,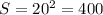 см
см
2. Знайдіть периметр прямокутника якщо його площа становить 98^2 а одна сторона удвічі більша за іншу
Розвязання
P=2(a+b) - периметр прямокутника
S=a* b - площа прямокутника,за умовою задачі b = 2*a нехай тоді одна сторона прямокутника дорівнює х а друга тоді буде 2х , моємо таке рівняння
2х*х=98
Тобто 1 сторона дорівнює 7 см, доті 2 сторона буде дорівнювати 7*2=14см
Знаходимо периметр
P=2(a+b)
Р=2(7+14)
Р= 42 см
ВСЕ