если сторона квадрата =а, то радиус окружности = (a√10) /4
Объяснение:
пусть сторона квадрата = а
∆ВЕF — ∆, вписанный в заданную окружность. → Центр окружности находим так: через середины сторон EF и ВЕ проводим перпендикулярные им прямые, точка О ( пересечение этих прямых) — центр окружности, радиус (R) которой требуется определить.По теореме синусов: ВЕ/sin(<F) = EF/sin(<B) = BF/sin(<E) = 2*R → R = BF/2sin(<BEF)По теореме Пифагора: BF^2=СF^2+BC^2 , так как F - середина СD, то СF=a/2, ВС=а → BF = √(a² + a²/4)=√(5a²/4)=(a√5)/2EF||BC и прямая EB — секущая → < ABD + <BEF =180°, <ABD=45°(так как ВD-диагональ квадрата) → <ВЕF=180°-45°=135°R = BF/2sin(<BEF) =( (a√5)/2 ) / sin(135°)=
Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
если сторона квадрата =а, то радиус окружности = (a√10) /4
Объяснение:
пусть сторона квадрата = а
∆ВЕF — ∆, вписанный в заданную окружность. → Центр окружности находим так: через середины сторон EF и ВЕ проводим перпендикулярные им прямые, точка О ( пересечение этих прямых) — центр окружности, радиус (R) которой требуется определить.По теореме синусов: ВЕ/sin(<F) = EF/sin(<B) = BF/sin(<E) = 2*R → R = BF/2sin(<BEF)По теореме Пифагора: BF^2=СF^2+BC^2 , так как F - середина СD, то СF=a/2, ВС=а → BF = √(a² + a²/4)=√(5a²/4)=(a√5)/2EF||BC и прямая EB — секущая → < ABD + <BEF =180°, <ABD=45°(так как ВD-диагональ квадрата) → <ВЕF=180°-45°=135°R = BF/2sin(<BEF) =( (a√5)/2 ) / sin(135°)== ((a√5)/2) / ((√2)/2 )= (a√5*√2) / (2*2) = (a√10) /4
Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: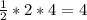 ед.²
ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
Прибавляем все значения. Это равняется 23 ед.²