Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1
Стороны оснований равны 8мм и 4мм. Угол C1CO = 45’
1.Вектор равный СО - это вектор
2. Длина этого вектора
3. Длина вектора С1О
4. Вектор С1О равен по длине вектору..

Показать ответ

Ответ:

bodisss

18.04.2022 12:04

$A_1A_3=12sin67,5^{\circ}\\ \\ A_1A_4=6\sqrt{8sin^267,5^{\circ}-1}\\ \\ A_1A_5=12\sqrt{2}sin67,5^{\circ}$

Объяснение:

Пусть O -- центр правильного многоугольника.

Если из точки O провести отрезки OA₁, OA₂,..., ОA₈, то получится 8 равных равнобедренных треугольников (по трём сторонам). Углы при вершинах этих треугольников будут равны и в сумме давать 360°. Тогда:

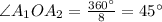
1. $\angle A_1OA_2=\frac{360^{\circ}}{8}= 45^{\circ}$

Рассмотрим ΔOA₁A₂:

A₁A₂ = 6, ∠O = 45°

∠A₁ = ∠A₂ (свойство р/б Δ)

$\angle A_1=\frac{180^{\circ}-\angle O}{2} =\frac{180^{\circ}-45^{\circ}}{2} =67,5^{\circ}$

Применим теорему синусов:

$\frac{A_1A_2}{sin\angle O}=\frac{A_2O}{sin\angle A_1}\\ \\ \frac{6}{sin 45^{\circ}}=\frac{A_2O}{sin67,5^{\circ}}\\ \\ A_2O=\frac{6sin67,5^{\circ}}{sin45^{\circ}}=\frac{6sin67,5^{\circ}}{\frac{1}{\sqrt{2}}}=6\sqrt{2}sin67,5^{\circ}$

2. A₁A₅ = 2A₁O = 2 * 6√2 sin67,5° = 12√2 sin67,5°

3. Рассмотрим ΔA₁A₃O:

∠A₁OA₃ = 2∠A₁OA₂ = 90°

A₁O = OA₃ = 6√2 sin67,5°

В р/б прямоугольном треугольнике гипотенуза равна катету, умноженному на √2, т.е.

A₁A₃ = √2 * 6√2 sin67,5° = 12 sin67,5°

4. Рассмотрим ΔA₁A₄A₅:

A₁A₅ = 12√2 sin67,5°, A₄A₅=6

∠A₁A₄A₅ = 90°

По теореме Пифагора найдём гипотенузу A₁A₄:

$A_1A_4=\sqrt{(A_1A_5)^2-(A_4A_5)^2}=\sqrt{(12\sqrt{2}sin67,5^{\circ})^2-6^2}=\\ \\ =\sqrt{144\cdot2sin^267,5^{\circ}-36}=\sqrt{36(8sin^267,5^{\circ}-1)}=6\sqrt{8sin^267,5^{\circ}-1}$

Сторона правильного восьмиугольника a1a2a3a4a5a6a7a8 равна 6. найдите диагонали a1a3 a1a4 a1a5

0,0(0 оценок)

Ответ:

anuta136

01.11.2021 04:45

Дано:

квадрат ABCD,

АС и ВD — диагонали,

угол ABO = 30 градусов,

диагонали АС и ВD пересекаются в точке О.

Найти угол ВОС — ?

Рассмотрим прямоугольник ABCD. Диагонали точкой пересечения делятся пополам. Значит треугольник АОВ еще является равнобедренным. Тогда угол АВО = углу ВАО = 30 градусов. Тогда

угол ОВС = угол В - угол АВО;

угол ОВС = 90 - 30;

угол ОВС = 60 градусов.

Треугольник ВОС является равнобедренным. Следовательно:

угол ОВС = углу ВСО = 60 градусов.

Зная, что сумма градусных мер углов треугольника равна 180 градусам. Получим:

угол ВОС = 180 - 60 - 60;

угол ВОС = 60 градусов.

ответ: 60 градусов.

0,0(0 оценок)

Популярные вопросы: Геометрия