Дана пирамида, у которой двугранные углы при основании равны.
Какие из утверждений верны?

-все рёбра пирамиды равны
-углы, которые образуют высота пирамиды с высотами боковых граней пирамиды, равны
-вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды
основанием пирамиды может быть произвольный треугольник

Объяснение: ЗАДАНИЕ 1

Если нужно найти угол В, то сумма острых углов прямоугольного треугольника составляет 90° поэтому угол В = 90-22=68°

ответ: угол В = 68°

ЗАДАНИЕ 2

Точно так же как и в 1- м задании: если угол В = 60°, то угол А=90-60=30°

Угол А=30°. Катет ВС лежит напротив этого угла и поэтому равен половине гипотенузы (свойство угла 30°). Значит гипотенуза АВ будет в 2 раза больше ВС: АВ=12×2=24; АВ=24

ОТВЕТ: АВ=24; угол А=30°

ЗАДАНИЕ 3

Так как катет ВС=160, а гипотенуза 320, значит катет ВС лежит напротив угла 30°, потому что он равен половине гипотенузы: 320÷2=160. Катет ВС лежит напротив угла А, значит угол А=30°, а угол В= 90-30=60°

ответ: угол А=30°, угол В=60°

ку) кр на 176 стр задание 5? :)

го хэлпану :

как мы знаем Sполная = Sбоковая + 2Sосновы.

у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.

рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=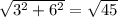см.

теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1=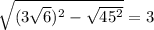 см. Теперь мы знаем высоту СС1=Н.

Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.

и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.

С тебя лайк :)