Цилиндр описан вокруг прямой треугольной призмы, основанием которой является прямоугольный треугольник c острым углом 30° градусов. вычислите объем призмы, если радиус основания цилиндра равен 10 см и диагональ большей боковой грани образует с плоскостью основания призмы угол 60° градусов
Объяснение:
Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:
c^2 = a^2 + b^2 (^2 - вторая степень числа)
Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)
a^2 = c^2 - b^2
Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2
В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ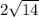
КМ и КН отрезок касательных проведенных из точки К к окружности с центром О.Найти КМ иКН если ОК=12 и угол МОН=120 градусам.
№2
Диагональ ромба ABCD пересекаются в точке О.Доказать что прямая ВD касается окружности с центром А и радиусом ОС
1. Отрезки касательных, проведенных из одной точки, равны, т. е. КМ=КН
КО - биссектриса угла МОН, след-но тр-ники КОМ и КОН - прямоугольные, с углами= 90, 60, 30 град.
ОМ=ОН=6см. , КМ=КН=sqrt(144-36)=7sqrt2
2. Диагонали ромба точкой пересечения делятся пополам, т. е. АО=ОС, отсюда диагональ ромба ВD касается окружности с центром А и радиусом ОС