Через вершину А правильного треугольника АВС проведена плоскость α параллельно стороне ВС так, что сторона АС составляет с этой плоскостью угол в 30°. Найдите длину проекции медианы AD треугольника АВС на плоскость α, если АВ = 12 см.

Объяснение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

1) прямая DC1 и плоскость A1B1C1

DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1  - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.

Рассмотрим ΔDС1D1 (∠D1=90°):  

D1C=A1B1=AB=5

DD1=AA1=12

tg ∠DС1D1 = D1D1/C1D1 = 12/5

∠DС1D1 = arctg (12/5)

2) прямая B1D и плоскость ABC

BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD  - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.

Рассмотрим ΔB1DB (∠B=90°):

BB1=AA1=12

BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:

BD² =AB²+AD²=25+49=74

tg ∠B1DB=BB1/BD=   = =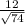

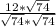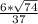
∠B1DB= arctg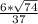

Объяснение:

1) угол NOM = углу FOE как вертикальные

по условию нам дано EO = ON и угол ONM = углу OEF

значит треугольники MON и EOF равны по второму признаку равенства треугольников

2) AB - общая сторона для треугольников ADB и ABC

и по условию у них CB=BD и равны углы ABD и CBA

значит треугольники ADB и CBA равны по первому признаку равенства треугольников

3) NK - общая сторона для треугольников NKP и NKM

также по условию MK=NP и MN=KP значит треугольники NKP и NKM по третьему признаку равенство треугольников