Через точки Р и R окружности с центром О проходят две касательные и пересекаются в точке K, образуя угол 120°. KО = 14 см. Найдите отрезки касательных.
​

Объяснение:

1.

<2=180-59=121

2.

Внешний угол треугольника равен сумме двух оставшихся углов не смежных с этим внешним углом :

109=<М+<Квнутр

109=63+<Квнутр

<Квнутр=109-63

<К внутр =46

<Квнеш =180-46=134

3.

<А:<В:<С=13:17:6

<А=13х

<В=17х

<С=6х

<А+<В+<С=180

13х+17х+6х=180

36х=180

Х=5

<А=13×5=65

<В=17×5=85

<С=6×5=30

а) треугольник остроугольный

б) С<А<В

В треугольнике против большего угла лежит большая сторона

АВ<ВС<АС

Против <В лежит сторона АС

Длинная сторона АС

4.

Если основание а =2,7cм ,то

Боковая сторона b=6,5 см

ответ : 6,5 см ; 2,7 см

Если основание а =6,5 см, то

Боковая сторона =2,7 см

ответ : 2,7 см ; 6,5 см. Но такого тр-ка не существует, т. к в треугольнике сумма двух сторон не может быть меньше третьей

2,7+2,7<6,5

5,4<6,5

5.

<А=60 <С=90 СМ - высота ВС=9,4 см

Найти : СМ

<В=180-<С-<А=180-90-60=30

Рассмотрим тр-к СВМ:

<СМВ=90 <В=30 ВС=9,4 см

Катет лежащий против угла 30 равен половине гипотенузе

СМ=1/2×ВС=1/2×9,4=4,7 см

6.

<ABM=x

<CBM=x+54

<СВМ+СВN=180

x+54+68=180

X=180-68-54

X=58

<ABM=58

<A=<ABM=58

<ABC=180-<A-<C=180-58-68=54

ответ : <А=58 <АВС=54 <С=68

(см. объяснение)

Объяснение:

Сразу замечу, что задача составлена неграмотно. Высота измеряется в сантиметрах, а не сантиметрах квадратных, поэтому правильного ответа здесь заведомо нет! Если пренебречь этой существенной неточностью, видим, что в последнем варианте не сокращена дробь, хотя .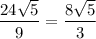

Комментарий:

Задачу можно было решить, не зная формулы Герона (хотя она есть в школьной программе).

Покажем, что достаточно уметь применять теорему Пифагора:

Решая систему, получаем, что .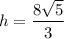

Однако такой подход, как мне кажется, менее оптимален.

Задание выполнено!