Чему равен радиус окружности вписанной в правильный треугольник со стороной 18 см? а)18√3 см б)9√3 в)6√3 г)3√3​

Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.​

Объяснение:

ΔОМА=ΔОМВ  как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)

По т. об отрезках пересекающихся хорд  АМ*МВ=СМ*МД

Т.к. СМ/МД=2/3 , то МД=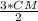 .  Получим √6*√6= СМ*   .

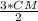СМ²=4, СМ=2 см .

Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).

d=5 см

=====================

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

ЗАДАЧА 1

1) треуг равнобедренный, где ав= вс=6

2)  в равноб треуг медиана является бис. и высотой. потому углы авд и двс= 120/2=60 град.

3)сумма углов треуг =180 град. в треуг авс

∠а+∠с= 180-120=60 град.

4) ∠а=∠с, тк треуг равноб.

значит ∠а=∠с=60/2=30

5) рассмотрим треуг авд.

он прямоугольный. по теореме катет, лежащий против угла в 30 град, равен половине гипотенузы. вд= 6/2=3

ответ: 3

задача 2.

1) рассмотрим треуг сдв.

он прямоугольный, ∠с= 180-90-45=45.

значит треуг равнобедренный, где сд= вд

2)рассмотрим реуг асд

он прямоуг, катет, лежащий против угла в 30 град, равен половине гипотенузы. сд= 8/2=4.

3)  сд= вд=4

ответ: 4

ЗАДАЧА 3

1) ТРЕУГ АВС ПРЯМОУГ. ЗНАЧИТ СВ= АВ/2= 10*2=20

2)сумма углов треуг =180, поэтому ∠в= 180-90-30=60

3) в треуг свд ∠с= 180-90-60=30

4) по теореме синусов вд/ sin 30 = вс/sin90

это вд/1/2= 10/1

2вд=10

вд=5

ответ: 5