Боковая поверхность правильной четырехугольной призмы имеет площадь 16 дм2.Диагональ основания призмы равна 4√ дм. Найдите площадь сечения призмы, проходящего через диагональ нижнего основания и противолежащую вершину верхнего основания.

Показать ответ

Ответ:

Алтын12938849к9ку9

01.02.2023 10:52

Пусть диагонали ромба пересекаются в точке О: АС ∩ ВD = О, диагонали ромба относятся как 3:4 ⇒ половины диагоналей ромба также относятся как 3:4 ⇒ можно обозначить: АО = 4х, ОВ = 3х. Периметр ромба равен 40 ⇒ его сторона равна 40 : 4 = 10,

АВ = ВС = СD = DА = 10. По теореме Пифагора:

АВ² = АО² + ВО² =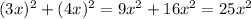 ${(3x)^{2} + (4x)^{2} } = {9x^{2} + 16x^{2} } = {25x^{2} }$ = 10² = 100 ⇒

x² = 100 : 25 = 4 ⇒ x = 2 ⇒ АО = 4х = 4*2 = 8, ОВ = 3х = 3*2 = 6,

AC = 2AO = 2*8 = 16, ВD = 2ОВ = 2*6 = 12. Площадь ромба равна:

S = 0,5 * AC * ВD = BH * AD ⇒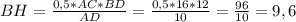 $BH = \frac{0,5*AC*BD}{AD} = \frac{0,5*16*12}{10} = \frac{96}{10} = 9,6$

ответ: высота ромба ВН равна 9,6

Диагонали ромба относятся как 3:4. Периметр ромба равен 40. Найдите высоту ромба.

0,0(0 оценок)

Ответ:

sharapoid

25.03.2023 15:51

Дуга AB = 49 градусов
дуга BC = 11 градусов
значит дуга CB = 60 градусов, но это минимальная из двух дуг, а если рассматривать душу в круге, которая большая, то душа CB = 360 - 60 градусов, значит угол, образуемый большей дугой CB, в вершине A - искомый и внутренний, значит равен половине дуги, опирающиеся на окружность,
значит угол САВ = (360 - 60)/2 = 150 градусов

Чёт фигово решаю, задачу, она вообще по другому решается. Дуга СА - и угол АBC - связаны, так, что Угол ABC опирается на дугу CA = 11. Значит Угол ABC- внутренний, и равен половине дуги в градусах, на которую он опирается, значит ABC = 11/2 = 5.5
Хорда ав стягивает дугу равную 49°,а хорда ас дугу в 11° найдите угол авс