АВСДА1И1С1Д1 - прямой параллелепипед в основание которого лежит ромб АВСД. Угол ВСД=60°, АВ=2, ДД1=2.Найдите тангенс угла между прямой ДВ1, и плоскостью ДСС1

Показать ответ

Ответ:

пупсень6

14.04.2020 00:52

План такой: найдем координаты векторов АВ, АС, ВС. Затем найдем длину векторов. После чего применим теорему обратную теореме Пифагора. Если она выполняется, то треугольник прямоугольный.

Чтобы найти координаты векторов, нужно из координат конца вектора вычесть соответствующие координаты начала вектора.
Вектор АВ = (3-6; 2-(-4); 3-3)
Вектор АВ = (-3; 6; 0)

Вектор АС = (3-6; -5-(-4); -1-3)
Вектор АС = (-3; -1; -4)

Вектор ВС = (3-3; -5-2; -1-3)
Вектор ВС = (0; -7; -4)

Длина вектора это квадратный корень из суммы квадратов координат вектора.
$|AB|= \sqrt{(-3)^2+6^2+0^2} = \sqrt{9+36}= \sqrt{45}\\ \\|AC|= \sqrt{(-3)^2+(-1)^2+(-4)^2} = \sqrt{9+1+16}= \sqrt{26}\\ \\|BC|= \sqrt{0^2+(-7)^2+(-4)^2}= \sqrt{49+16}= \sqrt{65}$

Теорема обратная теореме Пифагора. Если будет выполняться равенство
с²=а²+b², то треугольник прямоугольный.

$( \sqrt{65})^2= ( \sqrt{45} )^2+( \sqrt{26} )^2\\ \\65=45+26\\ \\65=71$

Равенство неверное. Следовательно треугольник АВС не является прямоугольным.

0,0(0 оценок)

Ответ:

Tanya11011

09.12.2020 20:53

Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.

Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей.

Диаметр вписанной в ромб окружности равен высоте ромба.

а) Для стороны ромба:

Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны.

4 АВ²= 16²+12²=256+144=400

АВ²=100 ⇒ АВ=√100=10.

б) Для высоты ромба:

Площадь ромба равна половине произведения его диагоналей.

S=12•16:2=96 см²

Площадь ромба равна произведению высоты на его сторону:

S=h•a; 96=h•10; h=9,6 ⇒ r=9,6:2=4,8 см

Из прямоугольного ∆ МОК искомое расстояние

МО=√(MK²-OK²)=√(64-23,04)=6,4 см

* * *

Формула объема шарового сектора V=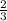 $\frac{2}{3}$ •πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара.

На рисунке приложения это КН.

∆ АОВ - прямоугольный, т.к. дуга АВ=90°

КО=АО•sin45°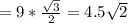 $=9* \frac{ \sqrt{3} }{2} =4.5 \sqrt{2}$ см

KH=R-OK=9-4,5√2=2,636 см²

V=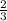 $\frac{2}{3}$ •π•81•2,636=142,346π см³

* * *

Пусть вершина конуса М, его высота МО, радиус ОА=5 см, хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М.

Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными перпедикулярно к АВ лучами МН и ОН.

Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°

$MO=6* \frac{ \sqrt{2} }{2} =3 \sqrt{2}$