Геометрия: Ас =12 см, угол в=40°, угол с=120° нужно найти ав; вс; угол а (20б)

Ас =12 см, угол в=40°, угол с=120° нужно найти ав; вс; угол а (20б)

Показать ответ

Ответ:

kiska510

14.11.2022 10:44

№1

Дано:

Угол АСВ=34°;

Угол СВР=18°;

Найти: угол АОВ.

Углы АСВ и АРВ – вписанные и опираются на одну и ту же дугу АВ, следовательно угол АРВ=угол АСВ=34°.

Сумма углов в любом треугольнике равна 180°.

Тогда угол ВОР=180°–угол ОРВ–угол ОВР=180°–34°–18°=128°.

Углы ВОР и АОВ – смежные, значит в сумме дают 180°.

Тогда угол АОВ=180°–угол ВОР=180°–128°=52°.

ответ: 52°

№2

Дано:

РNMO – равнобедренная трапеция, описанная вокруг окружности;

Точки А, В, С, D – точки касания;

Угол NPO=50°.

Найти: дуги АВ, ВС, СD, AD.

Углы при боковой стороне трапеции в сумме равны 180°, тогда угол РNM=180°–угол NPO=180°–50°=130°.

Углы при основании равнобедренной трапеции равны, то есть угол МОР=угол NPO=50°; угол OMN=угол PNM=130°.

Угол между двумя касательными, проведёнными из одной точки, равен разности 180° и градусной меры меньшей дуги, заключённой между данными касательными.

То есть:

Угол NPO=180°–дуга ВС => дуга ВС=180°–угол NPO=180°–50°=130°;

Угол МОР=180°–дуга CD => дуга CD=180°–угол МОР=180°–50°=130°;

Угол РNM=180°–дуга АВ => дуга АВ=180°–угол PNM=180°–130°=50°;

Угол OMN=180°–дуга AD => дуга AD=180°–угол OMN=180°–130°=50°.

ответ: 50°; 50°; 130°; 130°.

Геометрия 8 класс a=18b=34за данными малюнка знайдіть кут х2.Коло доторкається до сторін рівнобндерн

0,0(0 оценок)

Ответ:

Lyuda56

24.12.2020 09:29

$1) \ x = \sqrt{13} \\2) \ x = \sqrt{21} \\3) x_1 = 7, x_2=x_3 = 7\sqrt{2}$

Объяснение:

Обозначим неизвестные отрезки за x

1) неизвестный отрезок является гипотенузой прямоугольного треугольника:

$x = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$

2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным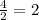 $\frac{4}{2} = 2$ :

$x = \sqrt{5^2 - 2^2} = \sqrt{25 - 4} = \sqrt{21}$

3) Здесь имеется три неизвестных отрезка, два из которых равны.

Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:

$x_1 = \frac{14}{2} = 7$

Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:

$x_2 = x_3,\\\sqrt{x_2^2+x_3^2} = 14 \\\sqrt{2x_2^2} = 14\\x_2\sqrt{2} = 14\\x_2 = \frac{14}{\sqrt{2} } = \frac{14\sqrt{2} }{2} = 7\sqrt{2}$