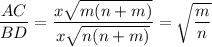Пусть трапеция АВСD и ее диагонали пересекаются в точке О. Если трапеция является равнобедренной, то прямая, которая проходит через середины оснований, перпендикулярна основаниям и длины диагоналей равны(свойство). Тогда прямоугольные треугольники АОD и ВОС (прямые углы АОD и ВОС - дано) равнобедренные и углы прилежащие к гипотенузам равны 45°. Следовательно, высоты этих треугольников ОН=АD/2, а ОР=ВС/2. Сумма этих высот равна высоте трапеции h. Площадь трапеции равна: S=(AD+BC)*h/2. AD+BC=36 (дано). Подставим в формулу площади значение h=OH+ОP=(1/2)(AD+BC) и получим:S=(AD+BC)*(AD+BC)/4 или 36*36/4=324.
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
Следовательно,