ΔABC — равнобедренный, AB=BC, ∡A+∡C= 87°. Определи величину∡A.

1. Назови равные углы в этом треугольнике (называй углы одной большой латинской буквой)

ΔABC — равнобедренный, AB=BC, ∡A+∡C= 87°. Определи величину∡A. 1. Назови равные углы в этом треугол

Показать ответ

Ответ:

prisheplub

23.07.2021 01:27

А) BADC - пирамида
1) Рассмотрим треугольник BAC. В нём M-середина BA и N - середина BC=> MN- средняя линия треугольника BAC(по свойству средней линии) MN || AC, MN=1/2AC
Аналогично, NP||CD и MP||AD => (MNP)||(ADC)(т.к. плоскости параллельны, если две пересек. в них прямых взаимно ||)
ч.т.д
б) Т.к. MN, NP, MP - средние линий соответственных ▲, то MN=1/2AC, NP=1/2CD, MP=1/2AD => ▲MNP подобен ▲ADC
А отношение площадей подобных ▲ равно квадрату коэффициенту подобия.
S1:S2=k^2
S2=S1:k^2
S2=48:2^2=12см^2
ответ:12 см^2

0,0(0 оценок)

Ответ:

Sheri1

13.07.2021 09:40

1) По теореме Пифагора:

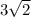$x^2 = 3^2 + 3^2\\\\x = \sqrt{3^2+3^2} = \sqrt{9+9} = \sqrt{18} = \boxed{3\sqrt{2}}$

ответ: $3\sqrt{2}$ .

2) По теореме Пифагора:

$10^2 = x^2 + 6^2\\\\x = \sqrt{10^2-6^2} = \sqrt{100-36} = \sqrt{64} = \boxed{8}$ .

ответ: 8.

3) Диагональ квадрата равна произведению его стороны на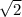 $\sqrt{2}$ , тогда:

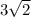$a = \dfrac{d}{\sqrt{2}} = \dfrac{6}{\sqrt{2}} = \sqrt{\dfrac{36}{2}} = \sqrt{18} = \boxed{3\sqrt{2}}$

ответ: $3\sqrt{2}$ .

4) По теореме Пифагора:

$8^2 + x^2 = 10^2\\\\x = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = \boxed{6}$ .

Площадь прямоугольного треугольника равна полупроизведению его катетов.

$S_{\bigtriangleup} = \dfrac{8\cdot 6}{2} = \dfrac{48}{2} = \boxed{24}$ .

ответ: 6; 24.

5) Треугольник равнобедренный (по условию). В равнобедренном треугольнике высота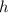 является биссектрисой и медианой. Образовавшиеся два треугольника являются прямоугольными. По теореме Пифагора:

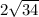$x^2 = h^2 + \left (\dfrac{12}{2}\right )^2 = h^2 + 6^2 = h^2 + 36\\\\x = \sqrt{h^2+36} = \sqrt{10^2 + 36} = \sqrt{100+36} = \sqrt{136} = \boxed{2\sqrt{34}}$

ответ: $2\sqrt{34}$ .

6) Катет, лежащий напротив угла с градусной величиной 30°, равен половине гипотенузы. Пусть - гипотенуза этого треугольника. По теореме Пифагора:

$c^2 = a^2 + x^2 =\\\\x = \sqrt{c^2 - a^2} = \sqrt{c^2 - \left (\dfrac{c}{2}\right )^2} = \sqrt{c^2 - \dfrac{c^2}{4}} = \sqrt{\dfrac{3c^2}{4}} = \boxed{\dfrac{c\sqrt{3}}{2}}$

Больше сделать здесь ничего нельзя, поскольку длина гипотенузы нам не дана. Но если бы она была дана, то длину катета можно было бы вычислить через эту формулу.