1) Пусть точка D - середина ребра СС₁, а точка Е - середина ребра АВ.
ΔAСD = BCD (по двум катетам), следовательно, АD = BD и ΔАDB - равнобедренный, в силу чего DE как медиана равнобедренного треугольника перпендикулярна АВ.
2) Согласно 4-ому признаку равенства прямоугольных треугольников ΔВED = ΔВCD, т.к. катет ВЕ = катету DC= 8, а гипотенуза ВD у этих треугольников является общей стороной.
Следовательно, катет ЕD = катету ВС = 16.
3) Площадь сечения плоскостью, проходящей через прямую АВ и середину ребра СС₁, - это площадь треугольника ABD, которая равна половине произведения основания АВ на высоту ЕD:
128
Объяснение:
1) Пусть точка D - середина ребра СС₁, а точка Е - середина ребра АВ.
ΔAСD = BCD (по двум катетам), следовательно, АD = BD и ΔАDB - равнобедренный, в силу чего DE как медиана равнобедренного треугольника перпендикулярна АВ.
2) Согласно 4-ому признаку равенства прямоугольных треугольников ΔВED = ΔВCD, т.к. катет ВЕ = катету DC= 8, а гипотенуза ВD у этих треугольников является общей стороной.
Следовательно, катет ЕD = катету ВС = 16.
3) Площадь сечения плоскостью, проходящей через прямую АВ и середину ребра СС₁, - это площадь треугольника ABD, которая равна половине произведения основания АВ на высоту ЕD:
S = АВ · ЕD : 2 = 16 · 16 : 2 = 256 : 2 = 128
ответ: 128
Дано: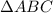
угол А = 48
угол В = 44
АD, BE, CF - биссектрисы пересекающиеся = О
_________________________
АОF - ?
Решение.
1) Т.к сумма углов треугольника равна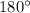
(по теореме о сумме углов в треугольнике), то угол С = 
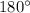- угол А - угол В = 
2) Т.к биссектриса делит угол пополам (по определению биссектрисы), то углы ЕВА и ЕВС =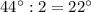
; углы FCA и FCB = 
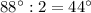; углы DAC и DAB = 
.
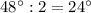3) Т.к сумма углов треугольника равна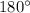
(по теореме о сумме углов в треугольнике), то угол АОС = 
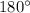- угол ОАС - угол ОСА = 
.
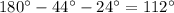4) Т.к сумма смежных углов равна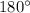
(по теореме о смежных углах), то угол AOF = 
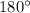- угол АОС =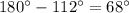
ответ: угол AOF = 68 градусов.