A, b, c — длины катетов и гипотенузы прямоугольного треугольника. Доказать, что: ab + ac + bc ≤ 2c^2

Показать ответ

Ответ:

sukhodolova

20.01.2020 15:23

а) ∠В = 30°, АВ=4 см, AD=ВD=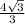 $\frac{4\sqrt{3} }{3}$ см ∠D=120°

б) S = 2√3 cм²

Объяснение:

а) Сумма острых углов прямоугольного треугольника равна 90°

∠В=90°-∠А=90°-60°=30°

Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.

⇒ АВ=2*АС=2*2=4см

По теореме Пифагора найдём катет ВС:

$BC=\sqrt{AB^{2}-AC^{2} } =\sqrt{4^{2}-2^{2} } =\sqrt{12} =2\sqrt{3}$

ВС = 2√3 см

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

$\dfrac{AB}{BC} =\dfrac{BD}{DC} \\\\\\\dfrac{4}{2} =\dfrac{BD}{2\sqrt{3}-BD } \\\\\\BD=4\sqrt{3} -2BD\\\\3BD=4\sqrt{3} \\\\BD=\dfrac{4\sqrt{3} }{3}$

Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=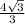 $\frac{4\sqrt{3} }{3}$ см

Так как сумма углов треугольника = 180°, то

∠АDB = 180-∠ВАD-∠В=180-30-30=120°

б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:

$S = \dfrac{1}{2} *BC*AC=\dfrac{1}{2} *2\sqrt{3} *2=2\sqrt{3}$

S = 2√3 cм²

В треугольнике ABC ∠C = 90°, AD – биссектриса, ∠A = 60°, AC = 2 см. а) Решите треугольник ABD ( ). б

0,0(0 оценок)

Ответ:

EseniaVoznesenskaya

30.08.2022 12:53

Дано В С
АВСН-трапеция / I I \
АВ=СН / I I \
угол А=60 А /__I I_ \ Н
К М
уголА=углуН( углы при основании равнобоковой трапеции равны)
Найти АВ=?
Решение
Из вершин меньшего основания проведем высоты ВК и СМ к нижнему основанию АН.
У нас получится два прямоугольных треугольника АВК и СМН
АВ и СН - гипотенузы. Гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны(первый признак). ВС=КМ
(противоположные стороны прямоугольника)
АК=МН АК+МН=10-4=6 АК=3
В треугольнике АВК угол АВК=180-90-60=30. Против угла в 30 градусов лежит сторона АК, равная половине гипотенузы АВ. АВ=6
ответ: АВ=6

0,0(0 оценок)

Популярные вопросы: Геометрия