8. Докажите равенство высот, проведённых к боковым сторонам в равнобе.
дренном треугольнике.
9. Докажите, что произвольная точка, лежащая на биссектрисе угла, равноуда-
лена от сторон угла.

Показать ответ

Ответ:

zelenukanna2002

02.01.2020 12:59

$\boxed{S_{ABC} = 3920}$ сантиметров квадратных

Объяснение:

Дано: ∠ACB = 90°, ∠ACE = ∠BCE, FE ⊥ CE, AF : FC = 3 : 4, BC = 56 см

Найти: $S_{ABC}$ - ?

Решение: Введем коэффициент пропорциональности x, тогда AF = 3x,

FC = 4x. Так как по условию ∠ACE = ∠BCE и ∠ACE + ∠BCE = ∠ACB, то

∠ACE = ∠BCE = ∠ACB : 2 = 90° : 2 = 45°. Рассмотрим прямоугольный (FE ⊥ CE по условию) треугольник ΔFEC. По теореме про сумму углов треугольника: ∠CEF + ∠FCE + ∠CFE = 180° ⇒ ∠CFE = 180° - ∠CEF - ∠FCE = 180° - 90° - 45°. Так как ∠CFE = ∠FCE = 45°, то по теореме треугольник ΔFEC - равнобедренный, следовательно FE = EC. Пусть CE = y, тогда

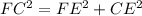FE = y. По теореме Пифагора: $FC^{2} = FE^{2} + CE^{2}$ .

$(4x)^{2} = y^{2} + y^{2} \\16x^{2} = 2y^{2}|:2\\8x^{2} = y^{2}\\y = x\sqrt{8}$

Проведем высоту к стороне FC из точки E в точку H. Рассмотрим прямоугольный (HE ⊥ FC по построению) треугольник ΔHEC.

$\sin \angle HCE = \frac{HE}{EC} \Longrightarrow HE = EC * \sin \angle HCE = EC * \sin 45^{\circ} = \frac{x\sqrt{8} \sqrt{2} }{2} = \frac{x\sqrt{16} }{2} = \frac{4x}{2} = 2x .$

Так как треугольник ΔFEC - равнобедренный, то по свойствам равнобедренного треугольника высота проведенная к основанию является биссектрисой и медианой, тогда FH = HC = FC : 2 = 4x : 2 = 2x.

AC = AF + FC = 3x + 4x = 7x. AH = AF + FH = 3x + 2x = 5x.

Треугольник ΔAHE подобен треугольнику ΔACB по двум углам так как угол ∠CAB - общий, а ∠AHE = ACB = 90°, тогда по свойству подобных треугольников: $\frac{AC}{AH} = \frac{BC}{HE} \Longrightarrow AC * HE = AH * BC$ .

$7x * 2x = 5x * 56 |: 2x\\7x = 140|:7\\x = 20$

AC = 7x = 7 * 20 = 140 см.

По формуле площади прямоугольного треугольника:

$S_{ABC} = \frac{AC * BC}{2} = \frac{140 * 56}{2} = 70 * 56 = 3920$ сантиметров квадратных.

В прямоугольном треугольнике ABC проведена биссектриса CE. Перпендикуляр к ней, проходящий через точ

0,0(0 оценок)

Ответ:

Асуна225

23.10.2022 21:09

tg∠FAM = 0,001

Объяснение:

Дано: ∠ACB = 90°, CM = MB, AB = 101, BC = 20,∠CAF = ∠BAF

Найти: tg∠FAM - ?

Решение: Так как по условию угол ∠ACB = 90°, то треугольник ΔACB - прямоугольный, тогда по теореме Пифагора:

$AC = \sqrt{AB^{2} - BC^{2} } = \sqrt{101^{2} - 20^{2} } = \sqrt{10 201 - 400} = \sqrt{9801} = 99.$

Так как по условию CM = MB и CM + MB = CB, то CM = MB = CB : 2 =

= 20 : 2 = 10. Рассмотрим прямоугольный (по условию ∠ACB = 90°) треугольник ΔACM. tg ∠CMA =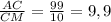 $\frac{AC}{CM} = \frac{99}{10} = 9,9$ . CB = CF + FB ⇒ CF =

= CB - FB = 20 - FB. По теореме о биссектрисе для треугольника ΔACB (AF - биссектриса по условию): $\frac{AC}{AB} = \frac{CF}{FB} \Longrightarrow AC * FB = AB * CF$ .

AC * FB = AB * (20 - FB)

99FB = 101(20 - FB)

99FB = 2020 - 101FB

200FB = 2020|:200

FB = 10,1

CF = 20 - FB = 20 - 10,1 = 9,9.

Рассмотрим прямоугольный треугольник ΔACF. tg∠CFA =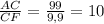 $\frac{AC}{CF} = \frac{99}{9,9} = 10$ .

Угол ∠CFA смежный с углом ∠BFA, тогда по свойству смежных углов

∠CFA + ∠BFA = 180° ⇒ ∠BFA = 180° - ∠CFA. Рассмотрим треугольник ΔFAM. По теореме про сумму углов треугольника:

∠FAM + ∠AFM + ∠FMA = 180°;

∠FAM + 180° - ∠CFA + ∠FMA = 180°;

∠FAM = ∠CFA - ∠FMA

tg(∠FAM) = tg(∠CFA - ∠FMA) =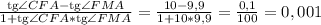 $\frac{\text{tg} \angle CFA - \text{tg} \angle FMA}{1 + \text{tg} \angle CFA*\text{tg} \angle FMA} =\frac{10 - 9,9}{1 + 10*9,9} = \frac{0,1}{100} = 0,001$ .