4. Дві сторони трикутника дорівнюють 18 см і 9 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?

Показать ответ

Ответ:

Fancyone

15.03.2023 11:10

Условие задачи некорректно. Иногда задачи с таким условием составляются специально. Доказательство ниже.

———

ВВ1 перпендикулярен плоскости альфа, следовательно, этот отрезок перпендикулярен любой прямой, проходящей в этой плоскости через В1.

BD=6√2

∆ ВАD- прямоугольный равнобедренный. Его острые углы равны 45°⇒

AD=BD•sin45°=6

По условию AD лежит в плоскости α.

Поэтому по т. о 3-х перпендикулярах В1А⊥AD, C1D⊥DA, проекция квадрата ABCD на эту плоскость – прямоугольник АВ1С1D.

Угол В1АD- прямой.

Угол В1DА=60°(дано)

Проекция диагонали ВD на плоскость α – гипотенуза В1D

треугольника В1АD

B1D=AD:cos60°=6:1/2=12

———————

Мы получили проекцию наклонной ВD, которая имеет большую длину, чем сама наклонная. Т.е. в прямоугольном ∆ ВВ1D длина катета B1D больше длины гипотенузы BD, чего быть не может. Задача с таким же условием есть от 2015 г, и так именно задумана её составителями.

Но если величина угла В1DА равна 30°,то проекция ВD на плоскост α равна AD:cos30°=4√3.

Или угол В1DB=60° -тоже получится допустимый результат.

Через строну ad квадрата abcd проведена плоскость а.из вершины b на эту плоскость опущен перпендикул

0,0(0 оценок)

Ответ:

YourTeaa

06.11.2021 03:48

ответ:

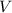призмы = 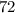см³.

Объяснение:

Обозначим данную призму буквами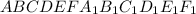 ABCD E F A_1B_1C_1D_1 E_1F_1 .

AD_1 = 8 см.

$\angle AD_1D = 30^{\circ}.$

============================================================

Если призма правильная, то она всегда будет прямой.

$\Rightarrow \triangle AD_1D$ - прямоугольный, где D_1D - высота данной призмы.

Рассмотрим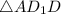 $\triangle AD_1D$ :

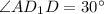$\angle AD_1D = 30^{\circ}$ , по условию.

Если угол прямоугольного треугольника равен $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow AD = \dfrac{AD_1}{2} = \dfrac{8}{2} = 4$ см.

По теореме Пифагора найдём высоту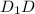 D_1D :

$D_1D^{2} = AD_1^{2} - AD^{2} = 8^{2} - 4^{2} = 48$

$D_1D = \sqrt{48} = 4\sqrt{3}$ см.

Рассмотрим нижнее основание данной призмы:

шестиугольник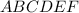 ABCD E F - правильный, так как данная призма тоже правильная.

- большая диагональ шестиугольника ABCD E F .

По свойству правильного шестиугольника,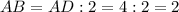 AB = AD : 2 = 4 : 2 = 2 см.

шестиугольника = $6 \cdot \dfrac{1}{2} \cdot AB \cdot AB \cdot sin(\dfrac{360^{\circ}}{6} )= 6 \cdot \dfrac{1}{2} \cdot 2 \cdot 2 \cdot sin(\dfrac{360^{\circ}}{6} )= 12 \cdot sin(60^{\circ}) = 6\sqrt{3}$ cм².