372. а) Ұзындығы 50,24 м шеңбермен шектелген дөңгелектің ау-
данын табыңдар. ә) Ауданы 50,24 м” дөңгелекті шектеп тұрған
шеңбердің ұзындығын табыңдар.

Показать ответ

Ответ:

08Dasha06

28.12.2020 05:38

3) AB параллельно CD значит угол BAC равен углу CDA - накрест лежащие.

р/м прямоугольные треугольники BFA и CED

угол BAD+ УГОЛ FBA =90 по теореме о сумме острых углов прямоугольного треугольника. УГОЛ CDE+угол ECD =90 по теореме о сумме острых углов прямоугольного треугольника. значит угол FBA= 90- BFA , а угол CDE=90-CED угол CED=углу BFA из выше доказанного, значит угол FBA =углу CDE

угол FBA =углу CDE

угол CED=углу BFA

AB=CD значит треугольник BFA = треугольнику CED по стороне и двум при лежащим к ней углам.

Вторую аналогично.

0,0(0 оценок)

Ответ:

makskolisnik9ouay08

02.03.2022 12:12

$\sqrt{2}$

Объяснение:

Начнем с того, что подкоренные выражения всегда больше или равны нулю, следовательно наименьшее значение корня, которое мы сможем получить=0.Но, данные выражения одновременно равны быть нулю не могут:

Доказательство: предположим, что оба корня равны нулю, значит: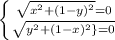 $\left \{ {{{\sqrt{x^{2}+(1-y)^{2}}=0 \atop {\sqrt{y^{2}+(1-x)^{2}\}=0 \right.$

$\left \{ {{{x^{2}+(1-y)^{2}=0 \atop {y^{2}+(1-x)^{2}=0 \right.$

$\left \{ {{x^{2}=0} \atop {(y-1)^{2}=0}} \right. \left \{ {{y^{2}=0} \atop {(x-1)^{2}=0}} \right.$

$\left \{ {{x=0} \atop {y-1=0}} \right. \left \{ {{y=0} \atop {x-1=0}} \right.$

$\left \{ {{x=0} \atop {y=1}} \right. \left \{ {{y=0} \atop {x=1}} \right.$

Мы можем увидеть, что x и y принимают разные значения в одном промежутке времени, а следовательно, обе части выражения не могут быть равны нулю, а следовательно возьмем одну пару из двух наименьших возможных значений: x=0,y=1:

$\sqrt{1^{2}+(1-0)^{2}}+\sqrt{0^{2}+(1-1)^{2}}=\sqrt{1+1}}+\sqrt{0+0}=\sqrt{2}$