№3. Все плоские углы при вершине S пирамиды SABCD равны 60°. Около этой пирамиды описан конус с радиусом основания √3 и вершиной S. На меньшей дуге BC, окружности основания конуса, выбрана точка P. Найдите расстояние от точки P до плоскости SAB, если объём пирамиды SABPCD наибольший.
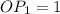 ед.
ед.
Объяснение:Конус описан около четырёхугольной пирамиды по условию.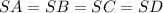 , как образующие конуса.
, как образующие конуса.
⇒ Боковые грани данной четырёхугольной пирамиды - равные равнобедренные треугольники
Так как боковые грани равны ⇒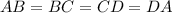
⇒ четырёхугольник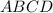 - квадрат
- квадрат
(Поясню, почему четырёхугольник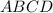 не может быть ромбом. Есть теорема и звучит она так : если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна
не может быть ромбом. Есть теорема и звучит она так : если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна 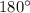 . Ромб - это параллелограмм, у которого противоположные углы равны. Поэтому если противоположные равны
. Ромб - это параллелограмм, у которого противоположные углы равны. Поэтому если противоположные равны 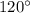 , к примеру, то их сумма
, к примеру, то их сумма 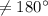 . Значит, ромб нельзя вписать в окружность)
. Значит, ромб нельзя вписать в окружность)
=======================================================
⇒ данная четырёхугольная пирамида - правильная.
Значит, её боковые грани - равносторонние треугольники, т.к. углы при вершине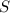 составляют по
составляют по 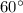 каждый.
каждый.
Из всех четырёхугольников, вписанных в окружность, наибольшая площадь у квадрата.
Также из прямоугольных треугольников с равной гипотенузой, наибольшая площадь у равнобедренного.
Найдём, при каком положении точки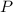 площадь основания наибольшая. Это будет середина дуги
площадь основания наибольшая. Это будет середина дуги 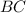 .
.
Значит, площадь пятиугольника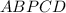 будет наибольшей.
будет наибольшей.
Тогда объём пятиугольной пирамиды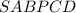 будет тоже наибольшим.
будет тоже наибольшим.
Обозначим на грани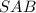 точку
точку 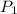 .
.
Так как точка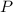 по отношению к грани
по отношению к грани 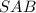 также расположена, как и точка
также расположена, как и точка 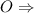
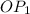 - расстояние от точки
- расстояние от точки
Радиус конуса равен половине диагонали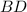 квадрата
квадрата 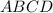 .
.
Так как боковые грани данной четырёхугольной пирамиды - равносторонние треугольники и они включают в себя по одной стороне основания данной пирамиды ⇒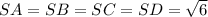 ед.
ед.
Найдём высоту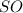 пирамиды
пирамиды 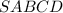 по теореме Пифагора:
по теореме Пифагора:
Проведём апофему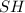 на сторону основания
на сторону основания 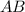 данной пирамиды. Т.
данной пирамиды. Т. 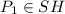 , т.к.
, т.к. 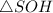 - прямоугольный, а
- прямоугольный, а 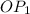 - высота данного треугольника.
- высота данного треугольника.
Найдём апофему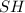 по теореме Пифагора:
по теореме Пифагора:
Рассмотрим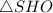 и
и 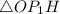 :
:
Теперь найдём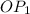 по теореме Пифагора:
по теореме Пифагора: