2. прямая т пересекает стороны тре-угольника abc ab в точке р, вс вточке e. угол abc = 35°, угол acb = 84°,угол ape = 119°.а) докажи, что прямые т и ас па-раллельны.б) найди внешний угол треугольни-ка abc при вершине а.
1) Пусть сторона основания равнобедренного треугольника равна х см, тогда боковые стороны равны (x+10) см. Зная, что периметр равнобедренного треугольника равен 98 см, составим уравнение
x + 2(x+10) = 98
x + 2x + 20 = 98
3x = 78
x = 26 см - сторона основания
Боковые стороны равнобедренного треугольника 26 + 10 = 36 см.
2) Теперь примем за х боковую сторону равнобедренного треугольника, тогда сторона основания равна (x+10) см. Составим уравнение
x + 10 + 2x = 98
3x = 88
x = 88/3 см - боковая сторона
88/3 + 10 = 118/3 см - сторона основания
Т.е. у обеих вариантов выполняется неравенство треугольника, значит данная задача имеет два решения.
1) Пусть сторона основания равнобедренного треугольника равна х см, тогда боковые стороны равны (x+10) см. Зная, что периметр равнобедренного треугольника равен 98 см, составим уравнение
x + 2(x+10) = 98
x + 2x + 20 = 98
3x = 78
x = 26 см - сторона основания
Боковые стороны равнобедренного треугольника 26 + 10 = 36 см.
2) Теперь примем за х боковую сторону равнобедренного треугольника, тогда сторона основания равна (x+10) см. Составим уравнение
x + 10 + 2x = 98
3x = 88
x = 88/3 см - боковая сторона
88/3 + 10 = 118/3 см - сторона основания
Т.е. у обеих вариантов выполняется неравенство треугольника, значит данная задача имеет два решения.
ответ: 26 см, 36 см, 36 см или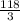 см,
см, 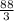 см,
см, 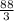 см.
см.
2 сосна
I
I 26м
I1 cосна
I I 10м
I I
II
30м
Соедини верхушки сосен, это будет искомое расстояние
После проведения линии получим наверху прямоугольный треугольник
вертикальный катет = 26 - 10 = 16(м)
горизонтальный катет = 30 м
Гипотенузу ( проведённую линию) найдём по теореме Пифагора:
Гипотенуза ^2 = 16^2 + 30^2 = 256 + 900 = 1156
Гипотенуза = √1156
Гипотенуза = 34 м
ответ: 34 м - расстояние между верхушками сосен.