15 радиус конуса равен 12 см, а высота - 9 см. шар проходит через окружность основания конуса и касается его боковой поверхности. найдите объем шарового сегмента, заключенного внутри конуса.
Смотри аналог с описанием решения (Если будет что-то не понятно, то пиши мне ❤️)
Объяснение:
Известна формула нахождения координат середины отрезка по координатам его концов:
xc = (xa + xb)/2, yc = (ya + yb)/2, где (xc; yc) – координаты точки С, которая является серединой отрезка AB.
В нашем примере даны координаты одного конца и середины отрезка. Воспользовавшись выше приведенной формулой преобразуем его для вычисления второго конца отрезка:
A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит
Объяснение:
vijohi8766
хорошист
20 ответов
2.9 тыс. пользователей, получивших
Смотри аналог с описанием решения (Если будет что-то не понятно, то пиши мне ❤️)
Объяснение:
Известна формула нахождения координат середины отрезка по координатам его концов:
xc = (xa + xb)/2, yc = (ya + yb)/2, где (xc; yc) – координаты точки С, которая является серединой отрезка AB.
В нашем примере даны координаты одного конца и середины отрезка. Воспользовавшись выше приведенной формулой преобразуем его для вычисления второго конца отрезка:
Xc = 2xb - xa, yc = 2yb - ya; xc = 2 * 6 - 6 = 6, yc = 2 * 6 – 4 = 8. C(6; 8).
Точка D — середина отрезка BC, поэтому xd = (xc + xb)/2, yd = (yc + yb)/2;
xd = (6 + 6)/2, yd = (8 + 6)/2; xd = 6, yd = 7. D(6;7).
ответ: C(6; 8); D(6;7).
A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит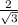
Объяснение: