1) В равнобедренном треугольнике ABC, BE - Высота, AB = BC
Найдите BE, если AC = и AB = 12

2) На стороне BC прямоугольника ABCD, у которого AB = 1.5, AD = 3.5, Отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED

3) В прямоугольном треугольнике a и b - катеты, c - гипотенуза. Найдите a, если b = и c = 0.9

4) Больший угол ромба равен 120 градусам, а меньшая диагональ его равна . Найдите площадь ромба

5) После совмещения двух квадратов со стороной 1 один из низ повернут относительно общего центра симметрии на 45 градусов. Найдите перемитр полученной фигуры.

6) Во сколько раз следует уменьшить сторону квадрата, чтобы его площадь уменьшилась в 4 раза?

Показать ответ

Ответ:

зика20

20.02.2022 20:21

(-2,2; -0,6)

Объяснение:

Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:

$\begin{cases}\sqrt{(x_0+4^2)+(y_0+3)^2}=3,\\\sqrt{(x_0+1)^2+(y_0-1)^2}=2.\end{cases}$

Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.

Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно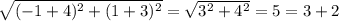 $\sqrt{(-1+4)^2+(1+3)^2}=\sqrt{3^2+4^2}=5=3+2$ . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо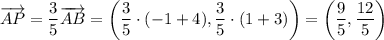 $\overrightarrow{AP}=\dfrac{3}{5}\overrightarrow{AB}=\left(\dfrac{3}{5}\cdot(-1+4),\dfrac{3}{5}\cdot(1+3)\right)=\left(\dfrac{9}{5},\dfrac{12}{5}\right)$

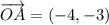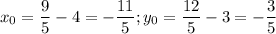Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор $\overrightarrow{OA}=(-4,-3)$ , мы получим координаты точки P(x₀, y₀): $x_0=\dfrac{9}{5}-4=-\dfrac{11}{5}; y_0=\dfrac{12}{5}-3=-\dfrac{3}{5}$ .

Решением системы является точка (-2,2; -0,6).

0,0(0 оценок)

Ответ:

lerakendrick

10.02.2020 04:24

Нам известно, что прямая y = kx + b проходит через точки с координатами А(- 1; 3) и В(2; - 1).
Исходя из этого мы составим и решим систему линейных уравнений.
3 = - 1 * k + b;
- 1 = 2k + b.
Решать систему будем методом подстановки. Выразим из первого уравнения системы переменную b.
b = 3 + k;
2k + b = - 1.
Подставляем во второе уравнение вместо b выражение 3 + k и решаем полученное линейное уравнение.
b = 3 + k;
2k + 3 + k = - 1.
3k = - 1 - 3;
3k = - 4;
k = - 4/3 = - 1 1/3.
Система:
b = 3 + ( - 1 1/3) = 5/3 = 1 2/3;
k = - 1 1/3.
Запишем уравнение прямой проходящей через заданные точки:
у = - 1 1/3х + 1 2/3.
ответ: у = - 1 1/3х + 1 2/3.

0,0(0 оценок)

Популярные вопросы: Геометрия