1. в правильную треугольную пирамиду вписан конус. найти площадь боковой поверхности этого конуса, если известно, что боковые грани пирамиды наклонены к плоскости основания под углом в 60 град. и радиус круга, вписанного в основание пирамиды, равен 16. 2. определить tg(бета), где (бета) - внутренний угол правильного шестиугольника. решить и понять суть , заранее .
Решение в приложенном рисунке
Попробовал расширение JPG - не
1 Площадь боковой поверхности конуса равна пи*радиус основания(r)* апофему(l)(отрезок соединяющий точку окружности основания и вершину конуса). Радиус основания =16 по условию. Апофему находим через определение косинуса. Высота конуса, апофема и радиус основания образуют прямоугольный треугольник с углами 90, 60 (по условию) и 30 градусов (сумма углов треугольника=180 градусов)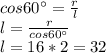
Площадь боковой поверхности=π*r*l=π*16*32=512*π
2 по определению-внутренние угль правильного шестиугольника=120 градусов