1. В окружности с центром в точке O и радиусом 8,1 см проведены диаметры AB и CD. Угол АOC равен 60°. До
кажите, что прямые AD и CB параллельны, и найдите
расстояние между ними.

Показать ответ

Ответ:

NHatynceva

10.09.2022 01:42

Чтож, попробую. Найдем сначала сторону ромба. Так как периметр равен сумме 4-х одинаковых сторон, то, обозначив сторону ромба за а, получим

Р=4*а

72=4*а

а=72:4

а=18.

По известной формуле площади ромба

$S=a^2*\sin\alpha$

где а - сторона ромба,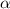 $\alpha$ - угол между двумя его сторонами. Причем угол любой (тупой или острый - синус будет один и тот же).

Найдем синус, подставив известные площадь и сторону.

$156=18^2*\sin\alpha$

Сократим обе части на 6

$26=3*18*\sin\alpha$

Сократим на 2 обе части

$13=3*9*\sin\alpha$

$\sin\alpha=\frac{13}{39}$

Если угол острый, то косинус положительный. По основному тригонометрическому тождеству

$\cos\alpha=\sqrt{1-\sin^2\alpha}$

$\cos\alpha=\sqrt{1-\frac{13^2}{39^2}}$

$\cos\alpha=\sqrt{\frac{1352}{39^2}}$

$\cos\alpha=\frac{\sqrt{1352}}{39}$

Тангенс - это отношение синуса к косинусу, то есть при остром угле

$\tan\alpha=\frac{13}{\sqrt{1352}}$

Если угол тупой, то косинус и тангенс будут с отрицательными знаками.

0,0(0 оценок)

Ответ:

Станислав2017

07.04.2021 19:57

Треугольник АВС, О -центр, ОН радиус перпендикулярный АВ в точке касания, ОК радиус перпендикулярный АС в точке касания,

четырехугольник АНОК, угол АНО+углуАКО=90, уголА=60, угол НОК = 360-90-90-60=120

треугольник НОК равнобедренный ОН=ОК=радиусу=1, проводим высоту ОР на НК, угол ОНК=углуОКН=(180-120)/2=30, треугольник ОКР прямоугольный, ОР=1/2 ОК - лежит напротив угла 30, ОР = 1/2=0,5, НР=РК= корень (ОК в квадрате - ОР в квадрате) =

=корень( 1-0,25) = 0,5 х корень3, НК =НР+РК= 2 х 0,5 х корень3 =корень3

треугольник АНК равнобедренный АН=АК как касательные к окружности. проведенные из одной точки, угол АНК=углуАКН = (180-60)/2=60, треугольник АНК равносторонний углы=60, значит АК=АН=НК=корень3

расстояние=корень3