1. Точка B делит отрезок AC в отношении 4 3. Точка C делит отрезок BD в ∶ отношении 5 7. В каком отношении точка C делит отрезок AD? Рассмотрите ∶
все случаи.
2. В скольких точках пересекаются 18 прямых, из которых ровно 3
параллельны друг другу и никакие три не проходят через 1 точку?
3. Проведите 8 прямых и отметьте на них 18 точек так, чтобы на каждой
прямой было отмечено ровно 5 точек.

Показать ответ

Ответ:

ромакравчук12

06.04.2021 03:46

Объяснение:

Дано:

АС = 13 см

ВD = 11 см

АВ = 9 см

Знайти: Р (АВСD) - ?

α - гострий кут між діагоналями

а² = b² + c² - 2bc *соs α

соs (180 - α) = - соs α

Розглянемо трикутник АВС по теоремі косінусів

АС² = АВ² + ВС² - 2 АВ * ВС * соs α

Розглянемо трикутник ABD

BD² = AB² + AD² - 2 AB * AD * соs α

∠A = ∠В = 180° BC = AD = x

Звідси маємо:

{13² = 9² + х² - 2* 9x* соs ∠В

{11² = 9² + х² - 2* 9x* соs ∠ А

{∠ А = 180° - ∠В => соs ∠ А = соs(180° - ∠В) = - соs ∠В

{169 = 81 + х² - 18x соs ∠В

{121² = 81 + х² + 18 x* соs ∠ B

Складемо рівняння (1) та (2)

290 = 162 + 2х²

128 = 2 х²

х² = 128 :2

х² = 64

х = 8 см

Периметр паралелограма дорівнює Р = 2 (9 + 8) = 34 (см)

Діагоналі паралелограма дорівнюють 13 см і 11 см, а одна зі сторін - 9 см. Знайдіть периметр паралел

0,0(0 оценок)

Ответ:

ryslan3222

01.05.2021 19:28

Решение.

ΔАВС , АС=7 см , ∠В=120° , Р=15 см .

Найти меньшую из неизвестных сторон .

Обозначит х=АВ , у=ВС .

По теореме косинусов имеем:

$AC^2=AB^2+BC^2-2\cdot AB\cdot DC\cdot cosB49=x^2+y^2-2xy\cdot cos120^\circ 49=x^2+y^2-2xy\cdot (-\dfrac{1}{2})49=x^2+y^2+xyx^2+y^2=49-xy\ \ \ \ (*)$

Так как периметр Р=х+у+7 , то х+у=Р-7 , х+у=15-7 , х+у=8 (см) .

По формуле квадрата суммы получим

$(x+y)^2=64\ \ ,\ \ x^2+y^2+2xy=64\ \ ,\ \ x^2+y^2=64-2xy$

Подставим в уравнение (*) выражение для х²+у² :

$64-2xy=49-xy\ \ ,\ \ \ 64-49=2xy-xy\ \ ,\ \ \ xy=15$

Теперь решим систему.

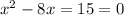$\left\{\begin{array}{l}x+y=8\\xy=15\end{array}\right\ \ \left\{\begin{array}{l}y=8-x\\x\, (8-x)=15\end{array}\right\ \ \left\{\begin{array}{l}y=8-x\\x^2-8x+15=0\end{array}\right\ \ \left\{\begin{array}{l}y_1=5\ ,\ y_2=3\\x_1=3\ ,\ x_2=5\end{array}\right$