Обозначим ∠А = α.
∠СВА = 90° - α (сумма острых углов прямоугольного треугольника равна 90°)
Тогда в прямоугольном треугольнике ВСН:
∠ВСН = 90° - ∠СВА = 90° - (90° - α) = α
Точка М симметрична точке В относительно точки Н, значит
СВ = СМ, Δ ВСМ - равнобедренный, тогда его высота СН является биссектрисой:
∠МСН = ∠ВСН = α
∠ОСК = ∠ВСА - (∠МСН + ∠ВСН) = 90° - (α + α) = 90° - 2α
АК = ВК по условию, значит ΔАВК равнобедренный,
∠КАВ = ∠КВА = α
∠СКВ = 2α как внешний для ΔАКВ (внешний угол треугольника равен сумме двух внутренних, не смежных с ним)
Если назвать угол иначе, то ∠СКО = 2α.
В треугольнике ОСК:
∠ОСК + ∠СКО = 90° - 2α + 2α = 90°, тогда
∠СОК = 90°, следовательно
ВК⊥СМ.
Ці точки лежать на серединному перпендикулярі точок та . Знайдемо координати точки — середини відрізка :
Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :
Коефіцієнт перпендикулярної прямої дорівнює . Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:
Тобто серединний перпендикуляр має формулу .
Знайдемо точку його перетину:
а) З віссю абсцисс:
Тобто точка має координати (3; 0).
б) З віссю ординат:
Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)
Відповідь:
а) (3; 0)
б) (0; –3)
Обозначим ∠А = α.
∠СВА = 90° - α (сумма острых углов прямоугольного треугольника равна 90°)
Тогда в прямоугольном треугольнике ВСН:
∠ВСН = 90° - ∠СВА = 90° - (90° - α) = α
Точка М симметрична точке В относительно точки Н, значит
СВ = СМ, Δ ВСМ - равнобедренный, тогда его высота СН является биссектрисой:
∠МСН = ∠ВСН = α
∠ОСК = ∠ВСА - (∠МСН + ∠ВСН) = 90° - (α + α) = 90° - 2α
АК = ВК по условию, значит ΔАВК равнобедренный,
∠КАВ = ∠КВА = α
∠СКВ = 2α как внешний для ΔАКВ (внешний угол треугольника равен сумме двух внутренних, не смежных с ним)
Если назвать угол иначе, то ∠СКО = 2α.
В треугольнике ОСК:
∠ОСК + ∠СКО = 90° - 2α + 2α = 90°, тогда
∠СОК = 90°, следовательно
ВК⊥СМ.
Ці точки лежать на серединному перпендикулярі точок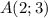 та
та 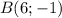 . Знайдемо координати точки
. Знайдемо координати точки  — середини відрізка
— середини відрізка 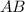 :
:
Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої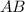 :
:
Коефіцієнт перпендикулярної прямої дорівнює . Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:
. Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:
Тобто серединний перпендикуляр має формулу .
.
Знайдемо точку його перетину:
а) З віссю абсцисс:
Тобто точка має координати (3; 0).
б) З віссю ординат:
Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)
Відповідь:
а) (3; 0)
б) (0; –3)