1. Найдите <С и < Д параллелограмма АВСД, если ВН┴ АД, АН = ВН.
2. Дан четырехугольник МРКТ (МР || КТ) диагонали которого
пересекаются в точке О. Найдите периметр треугольника КОТ, если МК =
20, РТ = 10, МР = 13, КТ = 13.
3. Дан параллелограмм АВСД. На сторонах ВС и АД взяты точки Н и О
соответственно так, что АВ = ВН = ОД, < АВН = 60. Найдите углы
четырехугольника АНСО.
Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.
Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей.
Диаметр вписанной в ромб окружности равен высоте ромба.
а) Для стороны ромба:
Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны.
4 АВ²= 16²+12²=256+144=400
АВ²=100 ⇒ АВ=√100=10.
б) Для высоты ромба:
Площадь ромба равна половине произведения его диагоналей.
S=12•16:2=96 см²
Площадь ромба равна произведению высоты на его сторону:
S=h•a; 96=h•10; h=9,6 ⇒ r=9,6:2=4,8 см
Из прямоугольного ∆ МОК искомое расстояние
МО=√(MK²-OK²)=√(64-23,04)=6,4 см
* * *
Формула объема шарового сектора V=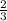
•πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара.
На рисунке приложения это КН.
∆ АОВ - прямоугольный, т.к. дуга АВ=90°
КО=АО•sin45°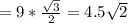
см
KH=R-OK=9-4,5√2=2,636 см²
V=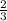
•π•81•2,636=142,346π см³
* * *
Пусть вершина конуса М, его высота МО, радиус ОА=5 см, хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М.
Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными перпедикулярно к АВ лучами МН и ОН.
Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°
V=S•h=πr²•h
V=π•25•3√2):3=π•25√2 см³
РА=РВ=РС=6 см
1. Рассмотрим Δ АОР - прямоугольный.
АО²+РО²=РА² - (по теореме Пифагора)
АО = √(РА²-РО²) = √(6² - (√13)²) = √(36-13) = √23 (см)
2. АО является радиусом описанной окружности.
R=(a√3) / 3
a= (3R) / √3 = (3√23)/√3 = √69 (см) - это длина стороны основы.
3. Находим периметр основы.
Р=3а
Р=3√69 см
4. Проводим РМ - апофему и находим ее.
Рассмотрим Δ АМР - прямоугольный.
АМ=0,5АВ=0,5√69 см
АМ²+РМ²=РА² - (по теореме Пифагора)
РМ = √(РА²-АМ²) = √(6² - (0,5√69)²) = √(36-17,25) = √18,75 = 2,5√3 (см)
5. Находим площадь боковой поверхности пирамиды.
Р = 1/2 Р₀l
Р = 1/2 · 3√69 · 2,5√3 = 3,75√207 = 3,75·3√23 = 11,25√23 (см²)
ответ. 11,25 √23 см².