1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.

Назови основные конструкции для построения треугольника GYF , равного данному треугольнику GEF .
Обрати внимание: эти треугольники имеют общую сторону GF .
РЕШИТЕ

Показать ответ

Ответ:

conyp2005

05.01.2020 11:15

Пусть AC - большая диагональ ромба; AC = d и острый угол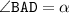 $\tt \angle BAD=\alpha$ . Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.

$\tt AO=OC=\dfrac{AC}{2}=\dfrac{d}{2};~~~\angle BAO=\angle OAD=\dfrac{\alpha}{2}$

Из прямоугольного треугольника AOD: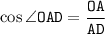 $\tt \cos \angle OAD=\dfrac{OA}{AD}$ отсюда выразим AD: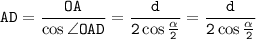 $\tt AD=\dfrac{OA}{\cos \angle OAD}=\dfrac{d}{2\cos\frac{\alpha}{2}}=\dfrac{d}{2\cos\frac{\alpha}{2}}$

Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.

$\tt h=AD\cdot\sin\alpha=\dfrac{d\sin\alpha}{2\cos\frac{\alpha}{2}}$ - высота ромба.

Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен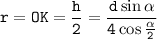 $\tt r=OK=\dfrac{h}{2}=\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}}$

Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды: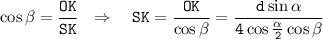 $\tt \cos \beta=\dfrac{OK}{SK}~~\Rightarrow~~~ SK=\dfrac{OK}{\cos \beta}=\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}\cos\beta}$

Найдем теперь площадь боковой поверхности пирамиды

$\tt S_{bok}=\dfrac{1}{2}\cdot P_{OCH}\cdot SK=\dfrac{1}{2}\cdot 4\cdot\dfrac{d}{2\cos\frac{\alpha}{2}}\cdot\dfrac{d\sin\alpha}{4\cos\frac{\alpha}{2}\cos\beta}=\dfrac{2d^2tg\frac{\alpha}{2}}{\cos\beta}$

Основание пирамиды - ромб с большей диагональю d и острым углом альфа. все двугранные углы при основ

0,0(0 оценок)

Ответ:

александра529

12.05.2021 01:15

Пусть

Дано:

АВСД р/б трапеция

Р (АВСД = 42 см

ВС - меньшее осн = 3 см

АС - биссектр уг ВСД

ВН - высота

ВН - ?

1) Т к по усл АС - бисс уг ВСД, то уг ВСА = уг ДСА,

2) уг ВСА и уг САД являются внутренними накрест лежащими при ВС||AD и секущей АС, значит уг ВСА = уг САД и = уг АСД, а значит тр АСД - р/б с основанием АС по признаку р/б треугольника.

3) т к по усл АВСД - трап - р/б , то СА = СД и = АС из п2

4) Р(АВСД) = 42 см

Р(АВСД) = АВ + ВС + СД + ДА = ВС + 3 АВ

42 = 3 + 3 АВ

39 = 3 АВ

АВ = 13 (см) = ВД = ДА

5) Т к трапеция АВСД - р/б , то АД = 2АН + ВС => AH = (13 - 3 ) : 2 = 5 см

6) Рассм тр АВН ( уг Н = 90*, по условию ВН - высота)

АВ² = ВН²+АН²

ВН² = 169 - 25

ВН² = 144

ВН = 12 см -искомая высота трапеции