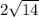1.Катеты прямоугольного треугольника 14дм и 48дм. Перпендикуляр к плоскости треугольника, восстановленный из вершины прямого угла, равен 60дм.
Найти расстояние от концов перпендикуляра до центра окружности, описанной около данного треугольника.
2.Из точки взятой вне плоскости, проведены к плоскости α перпендикуляр и наклонные. Одна из наклонных равна 12см и образует с перпендикуляром угол в 60º.
Найти проекции этих наклонных, если вторая наклонная имеет длину 10см.
его гипотенуза равна 25 (см), а 1 катет равен 7 (см), находим 2-й катет по теореме Пифагора: 25*25 (То есть 25 в квадрате) - 7*7 (7 в квадрате) = 625 - 49 = 576, а √576 = 24
То есть 24 (см) - это второй катет, и ещё одна сторона прямоугольника, ну и теперь путём несложным решений, (24+7)*2 = 62 (см) - это и есть периметр прямоугольника
Объяснение:
Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:
c^2 = a^2 + b^2 (^2 - вторая степень числа)
Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)
a^2 = c^2 - b^2
Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2
В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ