1. Даны векторы {4;−8}, {0;3}, {7;−1}, {1;−2}, {2;5} (a) Найдите все попарно коллинеарные вектора
(b) Найдите , такое что вектор {; 2,5} коллинеарен вектору
(c) Найдите координаты следующих векторов:
→− i. 3 →−
ii. 1,2 →−
iii. 0,6 →−
→− iv. 2 − 3 →−
→− v.2,3 −3 +2 −0,4
→−
→−
2. Даны точки (3; 4), (2; 4), (3; 7), (4; −2).
−→ −→ −→ −→ −→
(a) Найдите координаты векторов: , , , , −→ −→ −→ −→ −→
(b) Найдите длины векторов , , , ,
(c) Найдите координаты точек 1, 2, 3, 4 являющимися середи- нами отрезков , , , соответсвтенно.

3. 1) угол О= 180 - 50=130

2)угол А= (180 - 30):2=75

3)угол B= (180-120):2=30

4)угол О= 180 - 80=100

5)угол В= углу А

6)угол О= 180-100=80

7)угол А= (180-90):2=45

Объяснение:

1, 4, 6) треугольник АОВ равнобедренный, так-как радиусы круга равны, а у равнобедренного треугольника боковые стороны равны. Сумма углов треугольника равна 180 градусов, углы при основе равнобедренного треугольника равны между собой угол О равен сума углов треугольника(180 градусов) минус один из углов при основе и результат поделить на 2

9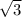

Объяснение:

Пирамиду можно разложить на треугольники, получится 4 равносторонних треугольника. Находим площадь одного треугольника и умножаем её на количество треугольников.

S=1/2*a*b*sin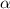 (Формула площади треугольника, где a и b - стороны треугольника, 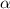- угол между этими сторонами).

Т.к. треугольник равносторонний, то можно заменить a*b на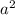 , а угол в равностороннем треугольнике всегда равен 60 градусам, а sin60 равен 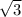/2 получаем формулу S=.

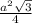Подставляем 3 и умножаем на 4. Четвёрки в числителе и знаменателе сокращаем и получаем S=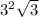=9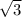.