1)Дан треугольник со сторонами 20 см, 34 см и 42 см.Данная точка P находится на расстоянии 25 см от всех сторон треугольника. Найти расстояние от точки P до плоскости треугольника. 2)Дан треугольник со сторонами 39 см ,17 см ,28 см. Точка S находится на расстоянии 6 см от плоскости треугольника и на одинаковом расстоянии от его вершин.Найдите расстояние от S до вершин треугольника.
РЕШИТЬ ХОТЬ 1 ЗАДАЧУ
24 см
Объяснение:
1) Пусть РО - расстояние от точки Р до плоскости (т.О ∈ плоскости, РО - высота пирамиды). Поскольку точка P находится на расстоянии 25 см от всех сторон треугольника, то т. О - центр круга, впис. в треугольник (r).
р=(20+34+42)/2=48
по формуле Герона S =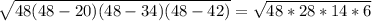 =
= cм²
cм²
r=S/p, r=336/48= 7 см
За т. Пифагора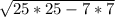 =
=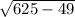 =24 см
=24 см
2) Поскольку т. S находится на одинаковом расстоянии от вершин треугольника, то т.О - центр круга, опис. навк.треугольника.
Далее аналогично: найти р = 42 , потом S по формуле Герона (S = 210), а потом найти R = 39*28*17/4*210=22,1
Далее использовать т. Пифагора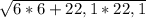 =22,9
=22,9