1. дан куб авсва1в1с1в1 с ребром а. найдите площадь сечения плоскостью, проходящей через: а) две его диагонали; б) середины трёх рёбер, исходящих из одной вершины; в) вершину b1 и середины рёбер ab и ad; г) диагональ ас1 параллельно прямой bd; д) середину ребра ab параллельно прямым bd и bcd. 2. дан правильный тетраэдр abcd с ребром а. найдите площадь сечения плоскостью, проходящей через: а) середину ребра ad параллельно плоскости abc; 6) вершину d и середины рёбер ab и вс; в) середину ребра ab параллельно рёбрам ac и bd; г) высоту dh тетраэдра параллельно ребру ac; д) центры граней abc, abd и bcd. 3. дана правильная четырёхугольная пирамида sabcd с верши- ной s. все рёбра пирамиды равны а. найдите площадь сечения плоскостью, проходящей через: а) середину ребра sa параллельно плоскости основания пирамиды; б) диагональ bd основания и середину ребра sc;

Показать ответ

Ответ:

Ramzi085

24.04.2023 16:35

Чтобы доказать,что данная фигура является квадратом,нужно,чтобы стороны были попарно параллельны и длина каждой стороны должна быть одинаковой. P.S. С данными точками четырехугольник не является квадратом. Ты скорее всего потерял(а) в точке C знак минус, то есть C(0,-8).

Для начала найдём векторы сторон,из которых состоит наш четырехугольник:(так как на сайте нет стрелочек над векторами,буду писать слово вектор или сочетание вершин например АВ)

Вектор AB = {-8-(-2);-2-6}={-6;-8}

Вектор BC = {0-8;-8-(-2)}={8;-6}

Вектор CD = {6-0;0-(-8)}={6;8}

Вектор DA = {(-2)-6;6-0)}={-8;6}

Чтобы проверить параллельны ли вектора,они должны быть коллинеарными,то есть отношения их координат должны быть равны одинаковому значению (назовем его k):

AB||CD? -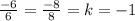 $\frac{-6}{6} =\frac{-8}{8} =k=-1$ .Следовательно AB||CD.

BC||DA? -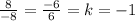 $\frac{8}{-8} =\frac{-6}{6} =k=-1$ . Следовательно BC||DA.

Теперь посчитаем длины векторов(Достаточно будет посчитать длины 2-х векторов,так как векторы коллинеарны):

|AB|=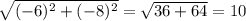 $\sqrt{(-6)^{2}+(-8)^{2} } =\sqrt{36+64} =10$ = |CD|

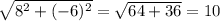|BC|= $\sqrt{8^{2} + (-6)^{2} } =\sqrt{64+36}=10$ = |DA|

Так как |AB|=10 и |BC|=10, то все четыре стороны равны. Следовательно,учитывая коллинеарность векторов и одинаковые длины, данный четырехугольник является квадратом.

0,0(0 оценок)

Ответ: