1.Центр окружности, вписанной в прямоугольный треугольник, находится на пересечении биссектрис углов треугольника.
Правда или нет?

2.Построение двух биссектрис треугольника будет достаточным, чтобы определить центр вписанной окружности.
Правда или нет?

3.В любую окружность можно вписать треугольник, так как биссектрисы углов любого треугольника пересекаются в одной точке.
Правда или нет?

4.Центр окружности, вписанной в прямоугольный треугольник, находится на его гипотенузе.
Правда или нет?

Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.

Объяснение:

Вписанная в окружность трапеция является равнобедренной.

Значит АВ=CD  стягивают равные дуги → ∪AB=∪CD

∠BOC=80° -центральный → ∪ВС=80°

∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD=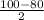 =10°.

∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.

∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )

Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD=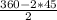 =135°

а) Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено условие:   боковые ребра пирамиды равны.

Длины сторон        

AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 6       0          0      36   6

BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²)  = -3      5,19615 0 36 6

CD = √((xD-xC)²+(yD-yC)²+(zD-zC)²)  = 0    -3,46410  2 16 4

AD = √((xD-xA)²+(yD-yA)²+(zD-zA)²  = 3     1,73205 2 16 4

AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²)  = 3    5,19615 0 36 6

BD = √((xD-xB)²+(yD-yB)²+(zD-zB)²)  = -3    1,73205 2 16 4 .

Как видим, в основании правильный треугольник и все боковые рёбра равны. Значит, пирамида правильная.

б) Основание апофемы пирамиды,лежащей в грани DAC, это середина стороны основания АС - точка Е.

Даны точки A(-1;0;1), C(2;3√3;1)

Е = ((-1+2)/2); (0+3√3)/2); ((1+1)/2)) =((-1/2); (3√3/2); 1).