Задання суммативного оценивания за 1 четверть по предмету «Физика» І вариант
1. Человек последовательно на север 3 км, на восток 4 км. Чему равен модуль перемещения?
А) 7 км
В) 3 км
C) 5 км
D) 1 км
E) 4 км
2. Скорость автомобиля за 20с уменьшилась с 20м/с до 10м/с. С каким средним ускорением двигался
автомобиль?
А) 0,5м/с2
В) 5м/с2
C) -5м/с2
D) -0,5м/с2
E) 50 м/с2
[1]
3. Выберите какая из формул соответствуют ускорению.
A) (v - vo) /t
B) 4APR
C) vo + at
D) v2R
E) S/t
F) vot + at-2
G) w-/R
4.Заполните таблицу:
[3]
Понятие
Определение
Объяснение нахождение расстояние до небесного
тела (только для горизонтального параллакса)
Афелий
Горизонтальный параллакс
5.Радиус-вектор бм задающий положение лошади, движущейся по окружности на арене цирка, повернулся
3
на угол
промежуток времени 4 с. Определите угловую скорость движения лошади и его
центростремительное ускорение.
[2]
6. Барабан стиральной машины при отжиме белья вращается равномерно с частотой 400 с Диаметр
барабана d = 40 см. Определите модуль линейной скорости точек на поверхности барабана и период
вращения барабана.
[3]
7. При эксперименте были измерены следующие значения:
Ng
t, c | S, ы
опыта
1
6 0.5
2
5.5 0,033
3
0.49 | 0,039
1) вычислите ускорение шарика при равноускоренном движении.
2) Вычислите значение перемещения шарика.
3) Вычислите время движения шарика.
3
2
а,
м/с2
8
8График показывает зависимость скорости от времени. По графику проекции скорости определите:
1) начальную скорость тела;
2)время движения тела до остановки;
3) ускорения тела;
4)вид движения(разгоняет тело или тормозит),почему?
5)запишите уравнение проекции скорости;
6)запишите уравнение координаты (начальную координату считайте равной нулю)

Показать ответ

Ответ:

dan4ik105217

24.12.2021 04:44

11,6 м

Объяснение:

Дано:

H = 4,5 м

R = 6,5 м

n = 1,33 - показатель преломления воды.

_____________

Rmax - ?

Сделаем чертеж.

Световые лучи обладают свойством обратимости. Поэтому будем считать, что на дне находится точечный источник света в точке S. Причем из этой точки лучи уже не выходят на поверхность (угол α - предельный угол полного внутреннего отражения)

Вычислим величину этого угла:

α = arcsin (1/n) = arcsin (1/1,33) ≈ 48,75°

Из треугольника ASO имеем:

tg α = x / H

x = H·tg α = 4,5·tg 48,75° ≈ 4,5·1,14 ≈ 5,1 м

Тогда:

Rmax = R + x = 6,5 +5,1 = 11,6 м

На поверхности водоема глубиной 4.5 м находится круглый плот, радиус которого равен 6.5 м. над центр

0,0(0 оценок)

Ответ:

Alex2103boec

19.05.2020 08:42

Моделируем камень точечной массой (точкой). Введём систему координат на плоскости с центром в точке-камне перед моментом броска. Ось y направлена вертикально вверх, ось x — ортогональна y в плоскости движения. Моменту броска присвоим время t=0.

Запишем ускорения точки (движение в поле силы тяжести):

$\ddot{x} = 0, \; \ddot{y} = -g$

Интегрируя, получим:

$\dot{x} = \int \ddot{x} dt = A$

$x = \int \dot{x} dt = A t + B$

$\dot{y} = \int \ddot{y} dt = - g \cdot t + C$

$y = \int \dot{y} dt = - g \cdot \frac{1}{2} t^2 + Ct + D$

Начальные условия:

$\dot{x}|_{t=0} = 0, \; \dot{y}|_{t=0} = v_0$

$x|_{t=0} = 0, \; y}_{t=0} = 0$

Отсюда:

$A = 0, \; B = 0, \; D = 0$

C = v_0

$\dot{x} = 0$

x = 0

$\dot{y} = - g \cdot t + v_0$

$y = - g \cdot \frac{1}{2} t^2 + v_0 t$

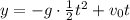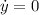Найдём экстремумы для $y = - g \cdot \frac{1}{2} t^2 + v_0 t$ , приравняв $\dot{y} = 0$ :

$- g \cdot t + v_0 = 0 \; \Rightarrow \; t^{*} = \frac{v_0}{g}$

Поскольку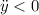 $\ddot{y} < 0$ , то полученный экстемум является максимумом для y(t) .

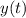Наибольшая координата y, достигаемая при моменте времени t*, и будет искомой высотой:

$y_{max} = - g \cdot \frac{1}{2} \left(t^{*}}\right)^2 + v_0 t^{*} = - g \cdot \frac{1}{2} \left({\frac{v_0}{g}}\right)^2 + v_0 \frac{v_0}{g}$

Принимая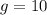 g = 10 м/с² и имея по условию 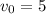v_0 = 5 м/с, получим:

$y_{max} = - \frac{1}{2} {\frac{{v_0}^2}{g}} + \frac{{v_0}^2}{g} = \frac{1}{2} {\frac{{v_0}^2}{g}} = \frac{1}{2} \cdot {\frac{{5}^2}{10}} = \frac{25}{20} = 1.25$ м.