Водних и тех же координатных осях постройте графики проекции вектора
скорости (на ось х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении а) начальная скорость 1 м. /с ускорение =0,5м/с в квадрате б) начальная скорость=1м/с а ускорение = 1м/с в квадрате в) начальная скорость 2м/с, а ускорение 1м/с в квадрате.
масштаб во всех случаях одинаков: 1 см - 1 м/с; 1 см - 1с.
с объяснением.
№1
S1x(t)=Vox*t+ax*t²/2; Vox=0; ax=2
S1x(t)=t²
V1x(t)=Vox+at=2t; V1x(15)=2*15=30 м/с
a1x=2 м/с²
--------------------------------
S2x(t)=Vx(15)*t=30*t
V2x(t)=30 м/с
а2х=0
---------------------------------------------
S3x(t)=(Vx²-Vox²)/(2aх); конечная скорость=0; начальная при торможении=30 м/с; S3=35 м; найдем ах.
35=-30²/2ах; 2ах=-900/35=-25,7; ах=-12,86 м/с²
S3x(t)=30*t-6,43*t²
V3x(t)=30-12,86t
ax=-12,86
-----------------------------
Vcp=весь путь/все время
S1=15²=225 м; S2=30*5=150 м; S3=35 м.
Найдем t3. V3=30-12,86*t=0
12,86t=30; t=2,3 c. За 2 с имея скорость 108 км/ч затормозить невозможно.
Vcp=(225+150+35)/(15+5+2,3)=18,4 м/с.
------------------------------------------------------
№3 Vx(t)=Vox+ax*t=4+8t.
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости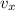
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории: